Lesson 8
1. Lesson 8
1.4. Explore 4
Module 6: Proportional Reasoning
In Lesson 7 you made conjectures about the relationships among scale factor, surface area, and volume.
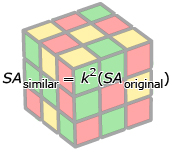
Turn to page 496 of the textbook and read “Connor’s Solution: Proving the conjecture for surface area” to see a proof of the surface area conjecture. (Connor’s solution appears in the first section of “Example 1: Reasoning about relationships among scale factor, surface area, and volume.”)
The relationships among surface area and volume of similar 3-D objects can be used to solve problems.
Read “Example 2: Solving a surface area problem” on pages 497 and 498 of the textbook to see how the relationship between scale factor and surface area can be used to determine how much glass is needed to create a replica of the Great Pyramid of Giza.

Hemera/Thinkstock
Did You Know?
The Great Pyramid of Giza is the largest pyramid ever built. It incorporates about 2.3 million stone blocks. The stone blocks weigh an average of 2.5 to 15 tons each! It is estimated that the workers would have had to set a stone block every 2.5 minutes.1
1 © National Geographic Society. Reproduced with permission.
For more information on the pyramids, search for “Egypt pyramids facts” using an Internet search engine.
Self-Check 3
Complete “Your Turn” on page 498 of your textbook. Answer
Return to pages 496 and 497 of the textbook and read “Isabel’s Solution: Proving the conjecture for volume” to see a proof of the volume conjectures you made in the last lesson. (Isabel’s solution appears in the second section of “Example 1: Reasoning about relationships among scale factor, surface area, and volume.”)