Module 6 Summary

Proportional reasoning can be used to help make some of the most important decisions in the moving process. Whether you are trying to determine which moving box is the best buy or which room is the best design for your big screen TV, an understanding of rates, scale diagrams, and scale factor is important.

 

In this module you investigated the following inquiry question:

• How can proportional reasoning be used to solve problems?

In the first few lessons you learned that the lowest rate is not always the best rate. The context of the situation determines whether you are looking for the lowest rate or the highest rate. For instance, in Canada fuel consumption is measured in L/100 km. When comparing two vehicles, the vehicle with the lowest L/100 km rate is the most fuel efficient. In the United States, fuel efficiency is measured in miles per gallon. In the U.S., the vehicle with the highest rate (mi/gal) is the most fuel efficient.

 

There are a variety of strategies that can be used to solve problems involving multiple rates or to use rates to solve for an unknown. Depending on the situation, you might have used any one of the following strategies to solve a rate problem in this module:

• unit analysis
• estimating using proportional reasoning
• equivalent ratios
• unit rates
• writing a function
• drawing a graph

In the last half of the module, you investigated how diagrams and models can be used to represent 2-D shapes and 3-D objects. You then discovered the relationships among scale factors, areas, surface areas, and volumes of similar 2-D shapes and 3-D objects. You discovered in your Math Labs that the

• area of two similar shapes are related by the square of the scale factor (k2)
  
  
• surface area of a similar object is related to the original object by the square of the scale factor (k2)
  
  
• volume of a similar object is related to the volume of the original object by the cube of the scale factor (k3)

 

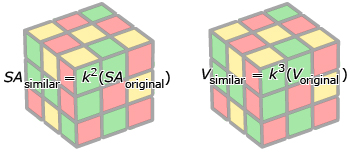
These relationships can be used to solve problems. For instance, you determined whether two shapes or objects were proportional, actual measurements from scale diagrams or models, and unknown dimensions.

 

As you have seen in this module, proportional reasoning is helpful in solving a variety of problems related to the moving process, from packing to shipping to unpacking.