Module 3
1. Module 3
1.19. Page 4
Module 3: Linear Measure
Bringing Ideas Together
In Explore you examined one type of linear measurement problem. In the examples and Self-Check activities that follow, you will meet a wide variety of measurement problems.
Example 1
Bill’s front door has a semicircular window, like the one in the photo, with a base length of 60 cm.

© Jenson/shutterstock
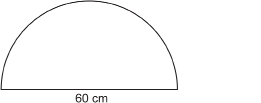
- Estimate the perimeter of the window.
- Calculate the perimeter, correct to the nearest centimetre.
Solution
- You must add the length of the semicircular curve to the 60-cm base of the window.
The length of the semicircular curve is one-half the circumference of a circle with the same diameter.
A circle with a diameter of 60 cm would have a circumference of about 3 × 60 cm or 180 cm.
So, the length of one-half of the circle, the semicircular curve, is about 90 cm (180 ÷ 2).
The perimeter of the window is about 90 cm + 60 cm = 150 cm.
- The circumference of a circle, if given the diameter, is C =
 d.
d.
So, the length of the semicircular curve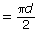 .
.
Therefore, the perimeter of this window is
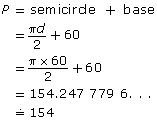
The perimeter of the window is about 154 cm. This answer is reasonable, since the estimated answer was
150 cm.
Example 2
Tracey is building a fence. The fence posts are 8 ft apart. Tracey will nail vertical spruce fence boards, which are ![]() in wide, across the 8-ft gap.
in wide, across the 8-ft gap.

- How many boards will Tracey use if she wants about a
 -in space between the boards?
-in space between the boards?
- How much space must Tracey allow on each side of her boards, if the boards are evenly spaced across the 8-ft gap?
Solution
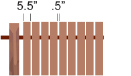
Each fence board plus a gap is
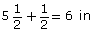
Two boards would be
6 in + 6 in = 12 in, or 1 ft
So, Tracey needs two boards for every foot within the 8-ft gap.
2 × 8 = 16 boards
In total, Tracey needs 16 boards.
- Since Tracey will use 16 boards, each with a width of
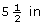 , the boards will cover
, the boards will cover
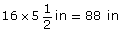
But, 8 ft between posts is
8 × 12 in = 96 in
So, the total for all the gaps between boards is
96 in - 88 in = 8 in
Now Tracey must allow for 17 gaps because there is a gap between the first board and the post.
So, the gap between boards must be
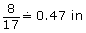
Note: 0.47 in is almost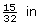 . So, Tracey can use her imperial tape measure to measure the gap for the fence boards.
. So, Tracey can use her imperial tape measure to measure the gap for the fence boards.
This answer is reasonable, since the gap must be slightly less than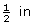 , or 0.5 in.
, or 0.5 in.
Example 3
The following diagram shows the layout of a running track.
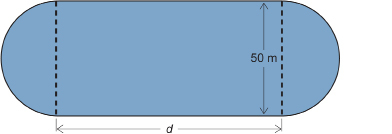
The ends are semicircles 50 m in diameter. The perimeter of the track is 400 m.
- Estimate the length, d, of each straight side. Note that, in this question, d does not represent diameter.
- Determine d to the nearest tenth of a metre.
Solution
View “Example 3 Solution.”
 Self-Check
Self-Check
When you are finished, check your answers.
SC 4. The diameter of a tennis ball is 6.5 cm. How many times will the ball roll to travel 10 m? Round your answer to a whole number of rotations. But, first, estimate your answer.

© Kelpfish/5695281/Fotolia
SC 5. A residential property has the shape of one quarter of a circular disk.
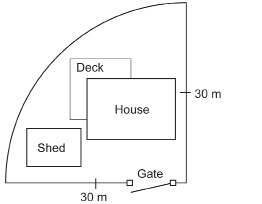
As a way of keeping his two dogs on the property, the owner plans to place a chain-link fence along the edge of the property. The chain-link fence costs approximately $8.00 per metre. What is the cost of fencing the property? Round to the nearest dollar.
SC 6. Jan has prepared a flower bed at one corner of her house. The flower bed is shaped as in the diagram.
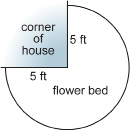
What is the perimeter of the flower bed? Round your answer to one decimal place. But, first, estimate your answer.
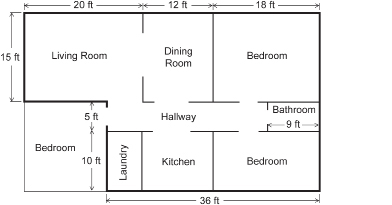
SC 7. The following are plans the Popowich family received from their building contractor for their new house.
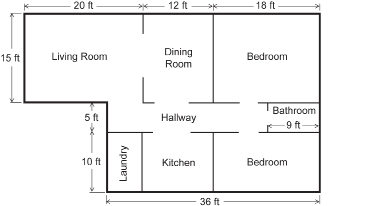
- What is the perimeter of their house according to these plans?
- After the Popowich family looked over the plans, the family considered adding an extra bedroom to the house according to this revision to the plans. What is the perimeter of their house according to the revised plans?
SC 8. Lumber sold as 1 × 6 boards actually have a thickness of ![]() and a width of
and a width of ![]() . The height of a stack of 1 × 6 boards is
. The height of a stack of 1 × 6 boards is ![]() . How many boards are there in the stack?
. How many boards are there in the stack?
 Mastering Concepts
Mastering Concepts
A 1-m length of wire is bent into a square. Another 1-m length of wire is bent into a circle.
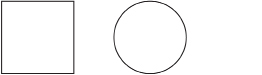
The diagram is not drawn to scale.
Determine which is larger, the side length of the square or the diameter of the circle. First use an estimation technique. Then base your answer on a more precise calculation.