Module 4

1. Module 4

1.25. Page 3

Mathematics 10-3 Module 4 Lesson 5

Module 4: Area

Explore

You will now explore the surfaces of a cylinder.

Try This

Work with a partner, if possible.

Step 1: Examine a soup can or any other can with a removable label. Remove the label by cutting the label along a vertical line. Flatten the label to form a rectangle.

This illustration shows the label from a soup can after it has been removed and laid flat. The width is labelled “height of the cylindrical can” and the length is labelled “length of the label.”

Step 2: Measure the length of the label and the radius of the circle on top of the cylinder with a ruler. Record this data in a table similar to the Circular Surface Measurements table shown.

Step 3: To measure the circumference of the circle top, use a string or roll the can one complete rotation, as shown in the demonstration “Can Circumference.”

Circular Surface Measurements

Item	Measurement
Length of Label
Radius of Circle
Circumference of Circle

TT 2. How does the length of the rectangular label compare with the radius and circumference of the circular surface?

Compare your results from TT 2 and the data recorded in the table with a partner or in a group.

What do you notice about the lengths of the label compared with the radius and circumference of the circular top and bottom?
Is there a relationship between the label length and the radius or circumference of the circle?
Is this relationship always true for any cylinder?

Compare your data with the data of someone in your group to see if the relationship is still true.

Summarize this relationship and place a copy in your course folder for future reference.

Self-Check

In this Self-Check activity you will assess your understanding of length relationships within the cylinder.

SC 1. Watch the animation “Constructing Cylinders,” and choose the correct answer.

Try This

You will now examine the net of a cylinder to help find the formula for the cylinder’s surface area.

TT 3. You saw in the Self-Check activity that the length of the rectangle is equal to the circumference of the circle end. If the radius of the cylinder is r units, what is the expression for the length of the rectangle?

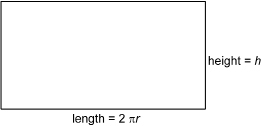
This illustration shows the rectangular part of a net for a cylinder. The width is labelled “height = h” and the length is labelled “length = 2πr.”

TT 4. If the height of the cylinder is h units, what is the formula for the area of the rectangular shape?

TT 5. In addition to the area of the rectangle, the surface area of the can also includes its two circular ends. What is the area of each circular end if the radius of the circle is r units?

TT 6. What is the total surface area of the can?

TT 7. Draw a net for a cylinder—the size doesn’t matter. Write the appropriate area formula on each part of your net. Measure the height and radius of your net. Calculate the area for each part of the net using your measurements. Cut out your net and tape it together to form a cylinder. The following diagram is just a guide.

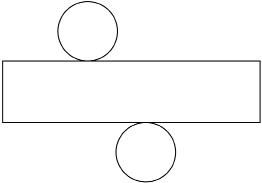
This illustration shows a net for a cylinder.

TT 8. Confirm your calculations from TT 7 using the “Right Cylinder” demonstration applet. Set the height and radius using the sliders to find the surface area. Then select the “Surface Area” button to see the formulas and calculations for each surface of the net.

Place your work from TT 3 to TT 8 in your course folder, and include any corrections.

In the previous sections you examined the surface area of cylinders. Now you will explore the surface area of a cone. Pay attention to the similarities and differences between the surface areas of these two 3-D objects.

Try This

If possible, work with a partner.

A cone-shaped paper cup is helpful for this activity. If you have a cone-shaped paper cup, start with Step 1. If you do not have a conical paper cup, start at Step 2.

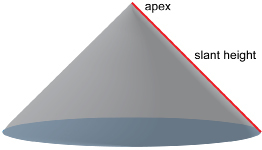
slant height: the shortest distance from the apex of a cone to its base along its curved surface

Step 1: Cut the cup along the slant height from the base to the apex.

This illustration shows a right circular cone with the slant height marked in red.

Flatten the cup to form a shape similar to the following illustration.

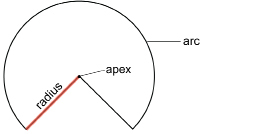
This illustration shows the net for a cylinder. It is an arc of a circle with each end of the arc joined to the centre of the circle by straight line segments. These line segments are identified as radii of the arc.

Study the cup in its flattened shape in order to answer the following question: How does the slant height s of the original cup compare to the radius of the flattened arc? Keep your thoughts in preparation for the Try This question that follows Step 2.

Step 2: Print the “Sample Net for a Cone.”

Cut out the sample net you just printed. Measure the radius of the arc.

Form the cone by pulling the straight line segments together. You may wish to tape the segments together to see that the paper forms a cone with a circular base.

Take measurements of the diameter of the base and the slant height. You will need these measurements for question TT 11.

TT 9. How does the slant height, s, of the original cone compare to the radius of the flattened arc?

TT 10. To what does the circumference of the original cone correspond when you look at the flattened cup?

Step 3: You will now determine the area of the original cone. Find the area of the flattened cup by comparing the flattened cup to a completed circle. The sector that completes the circle is coloured.

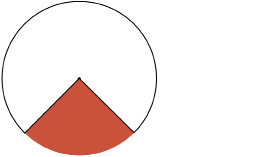
This illustration shows a circle with a sector filled in red.

TT 11. Complete “Area Table.” In the column “Your Value,” you will enter your measurements from the cone you formed in Sample Net for a Cone. Round to two decimal places.

Compare your table with the one shown in the Suggested Answers, or check your work with your teacher.

TT 12. Explain why the following is true.

area of conical cup = × area of completed circle