Print this chapterPrint this chapter

Module 5

1. Module 5

1.23. Page 3

Mathematics 10-3 Module 5 Lesson 5

Module 5: Angles

 

Explore

 

In this activity you will explore the relationships among angles formed when two parallel lines are intersected by a third line.

 

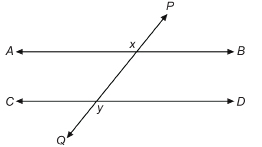
This illustration shows two parallel lines AB and CD cut by line QP at points x and y.

 

In the diagram intersects the parallel lines at points x and y. The goal of this activity is to determine relationships among the angles formed at x and y.

transversal: a line that cuts across two or more lines

 

The intersecting line is called a transversal.

 

Self-Check

 

SC 1. Look at the following diagram that shows a red line, a blue line, and a green line.

 

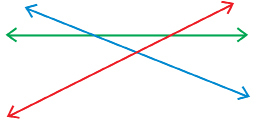
This illustration shows a red line, a blue line, and a green line. The red line crosses both the blue and green lines. The blue line crosses both the red and green lines. The green line crosses both the red and blue lines.

 

Which line or lines are transversals?

 

Compare your answer.

 

Try This

 

In this activity you will explore angles formed by a transversal. Share your work from this activity and place the information in your course folder. Work with a partner if possible.


Step 1: Take a blank sheet of paper and fold it twice to form two parallel creases when unfolded.

 

This illustration shows a sheet of paper with two parallel creases in it.

 

Self-Check

 

SC 2. Explain how you folded the paper and why, when unfolded, the creases are parallel.

 

Compare your answer.

 

Step 2: Fold the paper again but, this time, fold the paper vertically instead of horizontally. When unfolded, the crease

will cross both parallel creases. With the aid of a ruler, draw lines on the creases. Number the angles as shown in the

diagram.

 

This illustration shows a sheet of paper with two parallel creases in it and a third crease that crosses both of the parallel creases. The angles created are numbered from 1 to 8. The upper right angle is labelled 1, with the other three angles numbered 2, 3, and 4 going counterclockwise from angle 1. The bottom right angle is labelled 8, and the other three angles numbered 7, 6, and 5 going clockwise from angle 8.

 

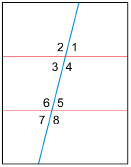
Step 3: Cut the sheet in two between the two sets of angles. One possible cut is the dashed line in the diagram.

 

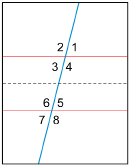
This illustration shows the sheet of paper from the previous illustration cut into two parts between the two parallel creases.

 

Step 4: Cut out the four angles—∠5, ∠6, ∠7, and ∠8—by cutting along the two intersecting lines that form the angles.

 

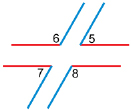
This illustration shows four angles (5, 6, 7, and 8) cut apart.

 

Step 5: Take ∠5 and compare the angle by placing it on each of ∠1, ∠2, ∠3, and ∠4. Are any of those angles congruent (the same measure) to ∠5? If there are congruent angles, list them in the following table.

 

Step 6. Repeat Step 5 for ∠6, ∠7, and ∠8.

 

TT 7. Complete a table like the following for Steps 5 and 6.

 

Angle

Congruent Angles from ∠1, ∠2, ∠3, and ∠4

∠5

 

∠6

 

∠7

 

∠8

 

 

TT 8. If all congruent angles are shaded the same colour, how many different colours would you need for this diagram? Explain your answer.

 

This illustration shows a sheet of paper with two parallel creases in it and a third crease that crosses both of the parallel creases. The angles created are numbered from 1 to 8. The upper right angle is labelled 1, with the other three angles numbered 2, 3, and 4 going counterclockwise from angle 1. The bottom right angle is labelled 8, and the other three angles numbered 7, 6, and 5 go clockwise from angle 8.

 

Share

 

How many colours would you need in TT 8? Make a visual representation by folding a new piece of paper or by drawing a new representation using a computer. Colour in all the angles that are congruent to each other with the same colour. Use as many colours as are necessary. How many colours did you need? Share your diagram or a photo of your diagram with your partner or group. How do your drawings compare?

 

Save a record of your discussion and your answers to TT 6, TT 7, and TT 8. Place your work in your course folder.