Lesson 2

1. Lesson 2

1.10. Explore 6

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

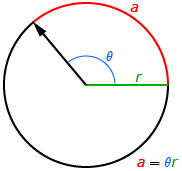
This is a sketch of a circle with the central angle labelled as theta, the subtended arc length labelled as a, and the radius of the circle labeled as r.

In Try This 4 you may have identified the relationship between arc length, radius, and central angle:

arc length = central angle in radians × radius of the circle

Using variables, this expression can be written as a = θr, where

a is the arc length
θ is the central angle in radians
r is the radius (arc length and radius are measured in the same units)

Read “Arc Length of a Circle” on page 173 of the textbook to learn more about why arc length can be determined using the formula a = θr.

In Try This 3 you determined how far the horse walked, or the arc length for a partial rotation around a circle. In Try This 4 you found the relationship between the length of an arc, radius, and central angle. In Try This 5 you will try to calculate the length of an arc when you know the central angle and radius of the circle.

Try This 5

This is a photo of the infield of a baseball diamond. Players are on the field and are playing baseball.

Comstock/Thinkstock

A baseball diamond can be thought of as part of a circle. At home plate, the central angle is 90° and the radius of the circle is 72 m, as shown in the diagram. Jane needs to build a fence around the outfield of a baseball diamond. The fence will follow the arc of the circle.

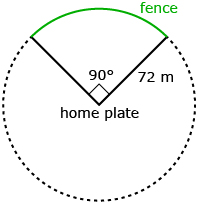
This is a sketch of a circle with a quarter of the circle drawn as a baseball diamond. Home plate is indicated at the centre of the circle and two radii are drawn from the centre to the edge of the circle with a length of 72 metres. The central angle created at home plate is 90 degrees. The arc on the circle across from the central angle and between the two radii is highlighted as the length of the fence.

Determine the length of the fence Jane needs to build. Explain your process.

Save your response in your course folder.

You may want to refer to Try This 3 or Try This 4 to see how you determined arc length.