Module 7

1. Module 7

1.4. Page 4

Mathematics 10-3 Module 7 Lesson 1

Module 7: Trigonometry

Bringing Ideas Together

trigonometry: the branch of mathematics based originally on determining sides and angles of triangles, particularly right triangles

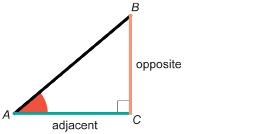
In Explore you examined the ratio in a right triangle of the side opposite to the side adjacent for a given acute angle. This ratio is an example of a trigonometric ratio. Trigonometry comes from two Greek words that mean “triangle measure.”

Did You Know?

More than 1000 years ago, Islamic mathematicians were using trigonometry to solve a variety of sophisticated problems.

In Explore, you saw that, for similar right triangles and a particular acute angle, the ratio was the same value regardless of the size of the right triangle.

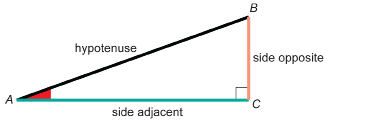
This illustration shows a right triangle ABC with angle A marked in red and angle C marked with a square. Side AC is labelled Side Adjacent and is green, side BC is labelled Side opposite and is orange, and side AB is labelled Hypotenuse and is black.

tangent ratio: the ratio of the length of the side opposite to the length of the side adjacent in a right triangle

This ratio is called the tangent ratio.

The tangent ratio is always in relation to an acute angle (in this case, the angle is ∠A). You must identify the acute angle when you write the tangent ratio in a particular situation.

So, tangent

This equation is often written more simply as .

Example 2

Draw a right triangle with an acute angle of 45°. Determine tan 45°.

Solution

It does not matter how large you draw the triangle, as all right triangles with a 45° angle will be similar in shape.

Once you draw the triangle, measure the opposite side and adjacent side.

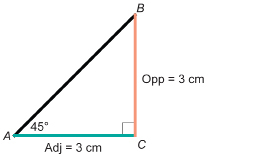
This illustration shows a right triangle ABC with angle A marked as 45 degrees and angle C marked with a square. The adjacent side is three centimetres long and the opposite side is three centimetres long.

A ratio of 1 means that, in a right triangle with a 45° angle, the opposite side and the adjacent side are always equal. For instance, if the opposite side were 10 cm, the adjacent side would also be 10 cm long, and .

Example 3

Determine tan 30°, correct to two decimal places, by measuring the sides of a right triangle.

View the animated “Tangent 30° Solution.”

Self-Check

SC 3. Use the method of the previous two examples to complete the following table. You may wish to use 10 cm for the adjacent side.

Angle	Side Adjacent	Side Opposite	Tangent
10°			tan 10° =
20°			tan 20° =
30°			tan 30° =
40°			tan 40° =
45°	10	10	tan 45° = 1
50°

Compare your answers.

Calculating the Tangent Ratio

Fortunately, it is possible to determine these ratios without actually having to draw a right triangle. You can also use your calculator. Yeah for technology!

Example 4

Find each tangent using your calculator.

tan 45°
tan 30°

Solution

There are several different ways in which angles may be expressed.

Be sure you have your calculator set to work in degrees.

To find tan 45°, press this sequence of keys. If you do not obtain the answer shown, consult your calculator manual or ask your teacher for help.

You should see something like this.

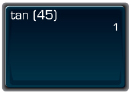
So, tan 45° = 1.
To find tan 30°, press this sequence of keys. If you do not obtain the answer shown, consult your manual.

You should see something like this.

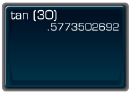
So, tan 30° = 0.577 350 269 2...

Self-Check

Use your calculator to complete the following table.

SC 4. Complete the following table. Round your answers to four decimal places.

Angle	Tangent
0
10°
20°
30°	0.5774
40°
45°
50°
60°
70°
80°

Compare your answers.

Solving Problems with the Tangent Ratio

In the next example, you will apply your calculator skills to help you solve a problem involving the tangent ratio.

Example 5

This photograph is of the Kwakwaka’wakw totem pole at Alert Bay, British Columbia.

Photo copyright SFU Museum of
Archaeology & Ethnology. Used with permission.

The Kwakwaka’wakw totem pole at Alert Bay, British Columbia, is one of the world’s tallest totem poles. The pole casts a shadow of 44.33 m in length along the ground when the angle of elevation of the sun is 50°, measured by using a clinometer. Calculate the height of the pole to the nearest metre.

Solution

Draw a diagram.

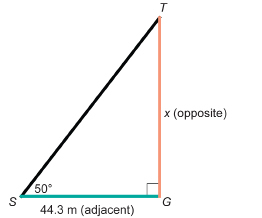
This illustration shows right triangle STG with angle G as the right angle. Angle S is 50 degrees; adjacent side SG is 44.3 m and opposite side TG has measure x.

Let x be the height of the totem pole.

The totem pole is perpendicular to the ground at G.

∠S at the tip of the shadow is 50°. This is the angle through which an observer would have to look up to see the sun just over the top, T, of the pole.

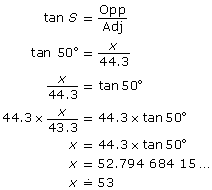
To calculate x, press these keys.

The totem pole is approximately 53 m high.

Self-Check

Use the method outlined in Example 5 to solve this question.

SC 5. Solve for x. Round to one decimal place.

This illustration shows right triangle ABC with angle C as the right angle. Angle A is 25 degrees; adjacent side AC is 10 cm, and opposite side BC has measure x.

Compare your answers.

Finding an Unknown Angle with the Tangent Ratio

You have just seen how an unknown side in a right triangle can be determined using the tangent ratio if you know the measure of an acute angle in that triangle. Can you solve problems going in the other direction? How could you find an unknown angle using the tangent ratio?

For instance, suppose you were told that the tangent of an angle in a right triangle were equal to 1. What would that angle be?

This illustration shows right triangle ABC with angle C the right angle. Angle A is filled with a red arc, side AC is labelled Adjacent, and side BC is labelled Opposite.

If tan A = 1, then then the opposite and adjacent sides must be equal so the ratio equals 1. Draw a right triangle with equal adjacent and opposite sides. Measure the angle and you will see that ∠A = 45°.

But if tan A = 2, what would ∠A be?

Example 6

If tan A = 2, determine ∠A to the nearest degree.

Solution

Method 1: Draw a right triangle, and measure the angle using a protractor.

Since and tan A = 2, then .

This means

opposite side = 2 × adjacent side

The size of the triangle will not matter, since all triangles for which tan = 2 will be similar triangles.

So, draw any right triangle with the opposite side half as long as the adjacent side. For instance, if the adjacent side = 5 cm, then the opposite side = 10 cm.

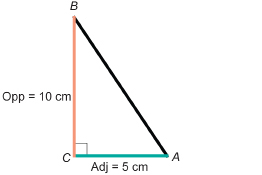
This illustration shows right triangle ABC with angle C as the right angle. Side AC is labelled Adj = 5 cm, and side BC is labelled Opp = 10 cm.

Measure ∠A with your protractor.

The measure of ∠A is approximately 63°. That is ∠A 63°.

This answer makes sense, knowing that tan 45° = 1. Because tan A = 2, ∠A must be larger than 45°.

Method 2: Use your calculator.

To find an angle from its tangent, strike these keys.

Your display should show 63.434 948 82 . . ..

So, ∠A 63°.

Note: The symbol tan−1 means you are working backwards from the ratio to find the angle. It is read “inverse tangent.”

You should write out your solution as follows.

Self-Check

Practise finding angles given the tangent ratio.

SC 6. Find ∠A given tan A = 0.5.

Use both methods as shown in Examples 4 to 6 to find the angle.

SC 7. Use your calculator to find each angle from its tangent. Round your answers to the nearest tenth.

tan A	∠A
0. 3456
4
0.827
2.5678

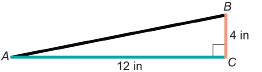
SC 8. A garage roof rises 4 in for a run of 12 in. To the nearest degree, what is the angle of the roof?

This illustration shows right triangle ABC with C the right triangle. Side AC has length 12 inches, and side BC has length 4 inches.

Compare your answers.

Mastering Concepts

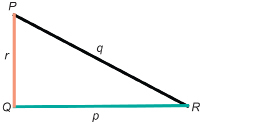
This illustration shows right triangle PQR with angle Q as the right angle. The side opposite angle R is labelled r, the side opposite angle Q is labelled q, and the side opposite angle P is labelled p.

Try this question. When you are finished, check your answer.

For ΔPQR, write the ratios for tan P and tan R.
How are ∠P and ∠R related?
How are tan P and tan R related?

Compare your answers.