Print this chapterPrint this chapter

Lesson 6

1. Lesson 6

1.1. Discover

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

Discover

 

Try This 1

 

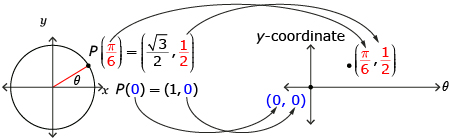
Take out the unit circle you made in Lesson 3: Try This 4. You were able to use this diagram to visualize angles and determine some trigonometric ratios. Another way to visualize some of the same information is to plot a graph of the y-coordinate of the intersection of the terminal arm and the unit circle, P(x, y), versus the angle θ of the terminal arm. Consider these examples:

  • When θ = 0, the y-coordinate of P is 0, so the point (0, 0) is plotted. (shown as blue in diagram)
  • When 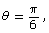the y-coordinate of P is 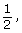so the point 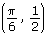is plotted. (shown as red in diagram)

    This diagram shows the point (1, 0) when the terminal arm of a unit circle is at zero. Arrows from the angle 0 and the y-coordinate 0 show the values of the angle 0 and the y-coordinate 0 corresponding to the point (0,0) on a coordinate grid. Similarly, the terminal arm intersects at the coordinate of the square root of 3 divided by 2, one half when the terminal arm is at the angle pi divided by 6. Arrows show the angle pi divided by 6 and the y coordinate of one-half corresponding to the point pi divided by 6, one-half on a coordinate grid.

Open Table and Graph Template.

  1. Complete the table for all angles on the unit circle you produced in Lesson 3: Try This 4.
  2. Graph the angle θ against the y-coordinate using the labelled axis provided.

course folder Save your completed copy of Table and Graph Template in your course folder.

 

Share 1

 

With a partner or group, discuss the following questions based on your graph created in Try This 1.

  1. What is the shape of the graph you produced?
  2. Could you extend this pattern for angles larger than 2π? If so, predict the shape of the graph.
  3. Could you extend this pattern for angles less than 0? If so, predict the shape of the graph.

course folder If required, place a record of your discussion in your course folder.