Print this chapterPrint this chapter

Lesson 4

1. Lesson 4

1.2. Explore

Mathematics 30-1 Module 5

Module 5: Trigonometry Applications and Identities

 

Explore

 

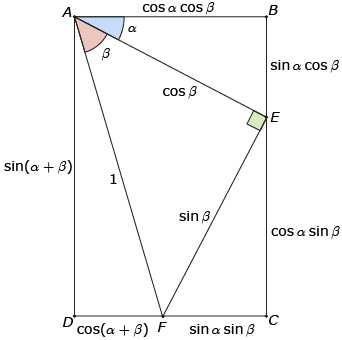
This diagram shows the diagram from Try This 1 and labels AB as the cosine of alpha times the cosine of beta, BE as the sine of alpha times the sine of beta, EC as the cosine of alpha times the sine of beta, CF as the sine of alpha times the sine of beta, FD as the cosine of alpha plus beta, AD as the sine of alpha plus beta, AE as the cosine of beta, and EF as the sine of beta.

In Try This 1 you may have drawn a diagram similar to the diagram shown here.

 

By recognizing that AD = BE + CE, you can predict the identity sin (α + β) = sin α cos β + cos α sin β. Similarly, because AB = DF + CF, cos α cos β = sin α sin β + cos (α + β). This second identity is often rewritten as cos (α + β) = cos α cos β − sin α sin β. These two identities are called sum identities. In Try This 2 you will use the sum identities to predict other identities.

 

Try This 2
  1. Explain why sin (−x) = −sin x and cos (−x) = cos x are identities.

  2. Use the sum identity sin (A + B) = sin A cos B + cos A sin B, and the identities from question 1 to show that sin (A − B) = sin A cos B − cos A sin B.

  3. Using a procedure similar to that of question 2, predict an identity for cos (A − B).

  4. Consider the special case where A = B for the identities sin (A + B) = sin A cos B + cos A sin B and cos (A + B) = cos A cos B − sin A sin B. Write simplified equivalent expressions for sin 2A and cos 2A.

course folder Save your answers in your course folder.



Two possible identities are

 

 

For the cosine sum, begin with

 

 

For the sine sum, begin with

 

 
An identity is cos (A − B) = cos A cos B + sin A sin B
Use the identities cos (−x) = cos x and sin (−x) = −sin (x) to rewrite the expression with positive B values.
Replace B with −B again.
Use the identities cos (−x) = cos x and sin (−x) = −sin x to rewrite the expression with positive B values.

Replacing every B with −B still makes the identity true.

 

 
Think of how the graph of sin x is transformed to give y = sin (−x) and y = −sin x.