Print this chapterPrint this chapter

Module 7

1. Module 7

1.42. Page 4

Mathematics 10-3 Module 7 Lesson 8

Module 7: Trigonometry

 

Bringing Ideas Together

 

In Explore, you investigated strategies for playing pentonimoes on a game board consisting of an 8 × 8 grid. There are 64 squares on the game board. Because each of the 12 pentominoes is made up of 5 squares, it is possible to place all 12 on the board with 4 squares left uncovered. This is because 12 × 5 = 60, and 64 – 60 = 4.

 

Variations of pentominoes are puzzles in which you are asked to completely cover a rectangle or square with pieces chosen from your set of 12 pentominoes. You can rotate the pieces you select, and you can flip them over, but you can’t overlap them.

 

For the next part of the lesson you will need to download a copy of -inch Grid Paper to make the square or rectangles on which to arrange your pentonimoes.

 

Example 1

  1. How many pentonimoes are needed to completely cover a rectangle with an area of 15 squares?

     
    This illustration shows a 3-square-by-5-square grid.

  2. Find at least one solution to this puzzle.

Solution

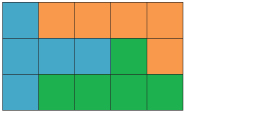
  1. There are 15 squares to cover. You will need 3 pentominoes, since 3 × 5 = 15.

  2. Here is one solution.

     
    This illustration shows pentominoes filling the 3-by-5 grid.

Now, puzzle these!

 

Self-Check

To answer these questions you will have to print at least two copies of -inch Grid Paper from which to cut the rectangles.

 

SC 6. Find one other way to cover the 15-square rectangle in Example 1.

 

SC 7. Find at least one way to cover a 4 × 5 grid completely.

 

SC 8.

  1. Could you create a puzzle in which you must cover a 4 × 7 grid completely with pentonimoes? Why or why not?

  2. List three sizes of grids you might be able to completely cover.

  3. What would the area of the largest grid be that could be completely covered with your 12 pentonimoes? List three possible grids with this area.

Compare your answers.

 

As you have seen in SC 1 and SC 2, you can only cover rectangles and squares with areas of multiples of 5. You might like to try a 5 × 5 grid, or a 5 × 6 grid, or even a 5 ×12 grid.

 

Mastering Concepts

 

When you have a problem, what type of strategies do you use to solve the issue? Here are some more common problem-solving strategies:

  • identify knowns and unknowns

  • use trial and error

  • look ahead and anticipate

  • work backwards

  • apply similar processes

  • look for patterns

  • make a systematic list

  • draw or model

  • eliminate possibilities

  • simplify the problem—get rid of extraneous data

  • search the Internet for help

In Lesson 7 you used tables to identify knowns and unknowns to help organize your known and unknown information. This strategy can help to simplify a problem by getting rid of extraneous information.

 

Can you think of another time you have used one of the listed strategies to solve a problem either in math or anywhere in your life?

 

What strategies have been used during this lesson?

 

Compare your answers.