Lesson 5

Discover

Try This 1

Consider the functions f(x) = x + 1 and g(x) = −x + 3.

1. 
   
   1. Predict what the graph of p(x) = (fg)(x) will look like. Explain how you made this prediction.
   2. Predict what the graph of 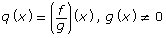will look like. Explain how you made this prediction.
2.  
   1. Use Multiply and Divide Functions to graph p(x) and q(x) and to check your predictions. Save screen captures of your two graphs.
      
      
       
      
   2. Explain how the graph of p(x) is related to the graphs of f(x) and g(x).
   3. Explain how the graph of q(x) is related to the graphs of f(x) and g(x).
3.  
   1. Use the equations of f(x) and g(x) to write an equation for p(x) and for q(x) in terms of x. Explain how you determined equations for p(x) and q(x).
   2. Are there any restrictions on x for p(x) or q(x)? Explain.
   3. Do the graphs of the equations you determined match the graphs from Multiply and Divide Functions? Should they?
4. Can the domain of p(x) or q(x) be determined from f(x)and g(x)? If so, explain how.

Save your responses in your course folder.

Share 1

With a partner or group, discuss the following questions based on the information in Try This 1.

1. How are multiplying and dividing functions similar? How are they different?
2. Compare multiplying and dividing functions to adding and subtracting functions. Describe both similarities and differences.

If required, save a record of your discussion in your course folder.