Lesson 6

Explore

In Try This 1 you combined P(s), a function that gave you a pet type given a student, and F(p), a function that gave you a food given a pet type. This combination gave the composite function, B(s), a function that gave the type of food to buy given a student. Combining functions this way is called a composition of functions. A composition of functions can be thought of as using the output of one function as the input of another function. In Try This 1 the output “pet” was used as an input to determine the food type. The following diagram shows how the functions from Try This 1 are related:

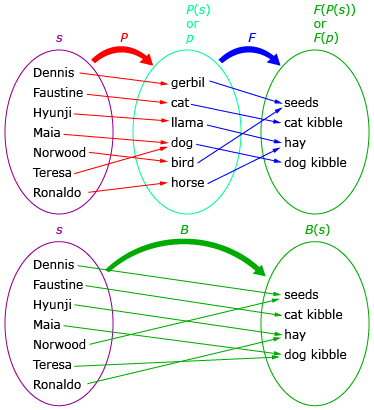
Three separate functions are shown, P, F, and B. These functions represent relationships between students, pets, and pet food. The s represents students; P(s) and p are both representations of pets, where P(s) is the type of pet determined from the student. F(P(s)), F(p), and B(s) all represent types of pet food, where F(P(s)) and B(s) are the type of pet food determined from a student, and F(p) is the type of food determined from the pet. Notice that F(P(s)) and B(s) have an equivalent meaning.

The most important thing to notice in the previous diagram is that F(P(s)) and B(s) are equivalent. Both F(P(s)) and B(s) represent the type of food to buy given the student. F(P(s)) is a composition of F(p) and P(s), so the output of P(s) (a pet type) is an input for F(p).

It is important to pay attention to the type of input for a function. For example, F(s) is not meaningful because F requires an input of a pet type and s is a student.

Sometimes a composition f(g(x)) is written This can be read as “f composed with g at x” or “f at g at x” or “f circle g at x.” In Try This 2 you will compose functions that are equations. Notice that the input and output for both functions are real numbers.