Week 24 - Hydraulic Systems and the Development of Mechanical Devices
Lesson 11
Lesson 11:
In this lesson we will examine the relationship between the size of the pistons in a hydraulic jack and their effect on the mechanical advantage the jack produces.
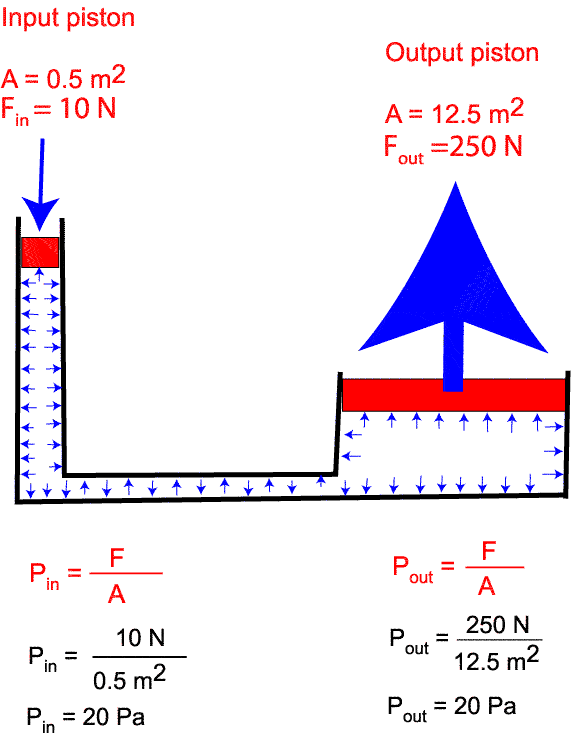
In the diagram below a force of 20 N is applied to the input piston. Pascal's law tells us that that force is then applied equally throughout the jack. So now the output piston is being pushed upward with a force of 20 N. (If we calculate the pressure (see below) we find the pressure is 20 Pa on each side.)
You will recall that a pascal is 1N of force spread over a square meter. Notice that the output piston has a larger area than the input piston so the amount of force it receives ends up being much larger than the force in the input piston. This creates a mechanical advantage .
Mechanical Advantage and Pressure
In an earlier lesson you learned that the formula for mechanical advantage is output force divided by input force. Examine the calculation below.
 |
We can see that the hydraulic jack in the diagram above has a mechanical advantage of 25. That's very high compared to other machines we have examined. |
But why such a large mechanical advantage? Because the pressure in the jack is applied equally over the whole vessel. Each and every square unit receives the same amount of force. The output piston has many more square units of area, therefore, it receives more force.
|
Still don't get it?
Here's an analogy. I agree to give every student in the school $5.00 each (they represent the number of square meters). In one room (the input piston) there is only 2 students so that room gets $10. But the next room (the output piston) has 30 students, that room gets $150.00 dollars. Money is like the force. The output piston gets more force because it has more area. |
Work In Equals Work Out
Do you remember when we talked about the idea that to get a certain amount of work out of a machine, you had to put the same amount of work into it in the first place. Well, hydraulic jacks are no different. Let's look at the formula for work again.
W = F x d
We want to lift the output piston on the jack 2 m. Now we can calculate the work that needs to be done.
W = F x d = 250 N x 2 m = 500 J of work
But how far do we have to push the input piston to get this much work done?
| W = F x d 500J = 10 N x d d = 500 N.m / 10 N d = 50 m |
Remember: 1 J = 1 N.m The Newton's cancel each other out in the equation, leaving us with metres. |
So now we know that to lift the output piston of our jack 2 m we must move the input piston 50 m. These input pistons are usually connected to motors, levers and pumps. You can generally hear these motors running when you are in a garage and see a car being jacked up on a hoist.
It is VERY IMPORTANT that you know what these mean and how to use them!
You will find most of the information related to these concepts on pages shown.
You will have to read and practice some questions to understand and REMEMBER how to do these.
You will find most of the information related to these concepts on pages shown.
You will have to read and practice some questions to understand and REMEMBER how to do these.
|
Pages
|
Term
|
Information
|
Equations and Examples
|
|
|
1
|
288-289
|
Work = W
(can be input or output) |
measured in Joules (pg. 289)
|
W = F x D
so answer is in N x (m or cm) ex. (W = 12Nm) |
|
2
|
294
|
Force = F
|
measured in Newtons (pg. 280)
A newton is the amount of force required to accelerate a mass of one kilogram at a rate of one meter per second squared. 1 N = 1 kg·m/s2 |
F = W/D involving work
or F = P/A involving pressure |
|
3
|
299
|
Area = A
|
measured in metric squared
used to help find pressure etc. ex. (cm 2 or m 2 ) |
ex. (A = 3 meters squared)
A = 3m 2 |
|
4
|
281
|
Speed Ratio = SP
|
just a number
|
SR = input distance/output distance
ex. (SR = 8cm/2cm = 2) |
|
5
|
281
|
Distance = D
|
measured in metric
|
ex. (D = 3meters)
D = 3m |
|
6
|
294, 295, 299
|
Pressure = P
|
measured in Pascals (pg. 294) or Newton (pg. 280) Meters
|
P in = F/A
or (depends in question) P out = F/A F = P in x A or (depends in question) F = P out x A ex. (P = 20N/4m 2 = 5N/m 2 ) |
|
7
|
280
|
Mechanical Advantage = MA
|
just a number
|
MA = output force/input force
ex. (MA = 12N/2N = 6) |
|
8
|
285
|
Efficiency = E
|
measured in percentage = % |
E = MA/SR x 100
ex. (E = 2/3 x 100 = 66%) |
|
9
|
285
|
E = Work output/work input x 100
ex. (E = 1200J/1600J x 100 = 75%) |
||
|
10
|
280-281
|
Input
|
force, distance, effort, etc
|
Part of equations
|
|
11
|
280-281
|
Output
|
force, distance, effort, etc
|
Part of equations
|
|
12
|
280
|
Ratio
|
is a fraction
|
ex. (F/A , W/D, 2/4, etc.)
|
|
13
|
294
|
Joules = J
|
measured in N x (m or cm)
1Joule = 1Newton x 1meter |
J = Nm
ex. (W = 12Nm) |
|
14
|
294
|
Pascals = PA
|
measured in N / (m 2 or cm 2 )
ex. (1 Pascal = 1Newton/meter squared) |
Pa = N/m 2
ex. (P = 5N/m 2 = 5 Pa) |
© 2002 Alberta Online Consortium