Lesson 3

1. Lesson 3

1.7. Explore 3

Mathematics 20-1 Module 1

Module 1: Sequences and Series

Self-Check 1

This is a play button that opens Interactive Venn Diagram.

In Try This 2 you found the sum of all the terms in a sequence (the total number of people in each row of the pyramid). This is referred to as an arithmetic series. Use Interactive Venn Diagram to verify the similarities and differences between arithmetic sequences and arithmetic series.

Try This 3

In Try This 3 you will work towards finding a formula to evaluate arithmetic series.

Part A

Follow these steps to evaluate the series 1 + 4 + 7 + 10 + 13 + 16 + 19.

Step 1: Evaluate the series by finding the sum of the terms on your calculator.

Step 2: Copy the series 1 + 4 + 7 + 10 + 13 + 16 + 19.

Step 3: Write the same arithmetic series underneath the original series from Step 2, but with the terms in reverse order (as shown).

This shows the arithmetic series 1+4+7+10+13+16+19. Underneath, the same series is printed in reverse order.

Step 4: Determine the sum of each column of terms. What do you notice?

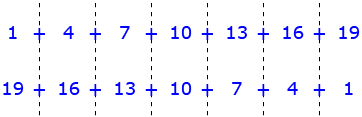
This shows the arithmetic series 1+4+7+10+13+16+19. Underneath, the same series is printed in reverse order.

Step 5: Multiply the number of columns by the sum of each column. Compare this sum with the sum you reached in Step 1.

What additional step should be applied to the answer in Step 5 in order to obtain the sum of the original arithmetic series?

Save your responses in your course folder.

Return to Discover and try using this new method to solve the problem in Try This 1. This will make a great record of your learning for this lesson.

Part B

You will use the method you used in Part A to derive a formula to find the sum of any arithmetic series.

Recall that the general term of an arithmetic sequence is tn = a + (n − 1)d.

For the arithmetic series 1 + 4 + 7 + 10 + 13 + 16 + 19, identify the parameters a and d.
When working with a series, think of n as the number of terms in the series. What is the value of n for this series?
Based on your answer from question 3, what would be the value of tn? What does tn represent in any series?
In the last steps of Part A, you applied the following operation to find the sum of the arithmetic series:

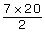
Substitute the parameters and variables you identified in Part B questions 1 to 3 for the numbers in the above expression.

For the number 20, which numbers did you combine to obtain this value?

In any series, tn will always be the value of the nth term.

You may want to refer to the sum of the series that you calculated in Step 1—this may help make the last step more obvious.