Lesson 4

Try This 1

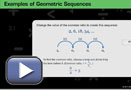
1. Work through Examples of Geometric Sequences. Find the common ratio, and then use the common ratio to extend each sequence.
   
   
    
   
   
   
   
2. Consider the following sequences.
   
   
    

   A	3, 15, 75, 375, 1875, …
   B	8, 12, 18, 27, …
   C	−5, −10, 20, 40, −80, −160, …
   D	1215, 405, 135, 45, …,
   E	2, 4, 8, 16, 32, 64, 128, 254, 508

   
   
   
   1. How are the first three sequences different?
      
      
   2. Which of the sequences are geometric? How do you know?

Challenging Assumptions

Not all sequences that appear to be geometric are, in fact, geometric. This lesson has assumed that if the first few terms of an infinite sequence show a geometric pattern, the rest of the sequence is also geometric.

Generally, the more terms a sequence shows, the safer it is to assume the sequence has a particular pattern. On the other hand, if only a few terms are shown, there may be other possible patterns governing the progression.

How many terms must be revealed in a sequence before you can confidently identify the sequence as geometric? Think about this as you complete Try This 2.

Try This 2

1. Consider the sequence 1, 2, …. What are some possible values for the next term in the sequence? State two possibilities and describe the reasons behind your choices.
   
   
2. Consider the sequence 1, 2, 4, …. Are there enough terms shown that you can be certain this is a geometric sequence? Can you find any other pattern in these three terms that would not result in 8 as the 4th term?

Save your answers in your course folder.

You will explore this concept further if you choose to complete Going Beyond later in this lesson.

Self-Check 1

Check your understanding by completing the following interactive activities:

• Create-a-Sequence
  
  
   
  
  
  
  
• Combining Sequences
  
  
   
  
  
  
  
• Identifying the Common Ratio