Lesson 5
1. Lesson 5
1.7. Explore 3
Module 1: Sequences and Series
Formula for a Geometric Series
You should have discovered that the formula for the sum of a geometric series can be expressed as
![]()
This is a good time to add the formula for the sum of a geometric series to your copy of Formula Sheet.
Note that one part of this formula is rn − 1. Do not mistake this for rn−1, which is an expression that you would find in the general term tn = arn−1. You should make a note of this in your copy of Formula Sheet.
Examine the variables in the formula for finding the sum of a geometric series.
![]()
![]()
Why is there a restriction on this formula that r ≠ 1? What happens if r = 1? Find out by replacing r with 1.
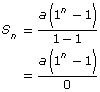
You can see that when r = 1, the denominator of the fraction becomes 0. This is undefined and is not possible. That is why r ≠ 1.
Can you create a geometric sequence where r = 1? What would the series look like? ![]()
Try This 3
Retrieve your work from Try This 1. In question 3.b. you had to determine the total sum of the grains of rice on 9 squares of a chessboard. Use the geometric series formula to confirm your answer from Try This 1.
You will need to identify the values for t1, r, and n. Substitute the appropriate values into the series formula, and then evaluate. Need a hint?
What is t1? ![]()
What is r? ![]()
What is n? ![]()
How do I substitute values? ![]()
How many grains of rice are there in total? ![]()
Mistakes can easily be made when working with negative numbers. Watch Evaluating a Power with a Negative Base to see a common error that arises when using the series formula to evaluate a power with a negative base, such as −23.
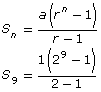
Sn = the sum of the first n terms of the geometric series
a = the first term of the geometric series
r = the common ratio
n = the number of terms in the geometric series
