Lesson 6

Geometric Sum Limit

 

In the Math Lab you may have discovered the following points about infinite geometric series:

• when the common ratio is greater than 1 or less than −1, a limit to the sum does not exist (r > 1 or r < −1, no limit)
  
  
• when the common ratio is between −1 and 1, the sum of the series does have a limit (−1 < r < 1, limit)

Self-Check 1

 

Complete Geometric Series: Sum or No Sum.

 

Try This 2

 

In previous lessons you constructed formulas based on arithmetic and geometric patterns. You derived formulas by studying specific examples and combining formulas. In this activity you will determine a formula for evaluating the sum of an infinite geometric series where a sum exists.

1. Choose any value for a common ratio, r, which would result in a convergent series.
   
   
2. Evaluate r10, r20, r50, and r100 on your calculator. What do you notice about the value of rn as n increases? What number does rn approach as n gets larger?
   
   
3. Substitute your result for rn from question 2 into the following formula:
   
   
    
   
   
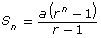
   What does the expression for Sn begin to look like as n increases?