Lesson 1

Discover

 

In Try This 1 you will gain experience with different definitions for the primary trigonometric ratios. These definitions involve circles—not triangles! Since a circle has 360°, circles allow you to determine cosines, sines, and tangents of angles between 0° and 360°. The math that allows you to consider angles greater than 90° will be discussed later in this lesson. The goal right now is to get experience with this new approach to cosine and sine.

 

Try This 1

 

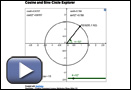
With a partner, use Cosine and Sine Circle Explorer to answer the questions below. The goal of Try This 1 is to get you thinking. Don’t worry if you can’t answer all of the questions.

 

There are two sliders you can use in this applet:

• Use the Radius slider (bottom left) to change the radius of the circle.
  
  
• Use the θ slider (bottom right) to change the angle shown. If you have trouble moving the slider precisely, click on the slider and use the arrow keys on your keyboard.

1. As θ increases from 0° to 90°, sin θ increases from 0 to 1. What happens to sin θ as θ increases from 90° to 360°?
   
   
2. What happens to cos θ as θ increases from 0° to 360°?
   
   
3. Use the Radius slider to make the radius of the circle 1.0. Then examine the cosine and sine of different angles. Why is a radius of 1.0 special?
   
   
4. Why does the equation cos θ = 0.2 have two solutions?

Save your responses in your course folder.