Lesson 1

1. Lesson 1

1.6. Explore 2

Mathematics 20-1 Module 2

Module 2: Trigonometry

Two Equal Heights on a Semicircle

Consider an engineer working on the Lune Aqueduct restoration project. The restoration of one of the semicircular arches with a radius of 5 m requires that anchors be installed. Installing the anchors requires using a special tool attached to a rotating boom. If the boom is positioned in the middle of the arch, at what angle must the boom rotate in a counterclockwise direction so that its endpoint is 4 m off the ground?

This situation can be modelled using a diagram.

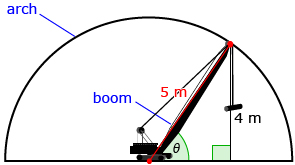
This diagram models the restoration project of a semi-circular arch with a radius of 5 metres and a boom height of 4 metres.

There is a second angle where the boom will be at a height of 4 m, as shown in the next diagram.

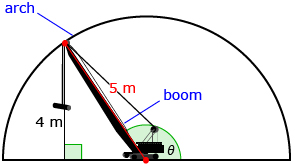
This diagram models the restoration project of a semi-circular arch with a radius of 5 metres. The boom is at a second location 4 metres above the ground.

As you can see from the two diagram models, there are two places where the boom could be found 4 m above the ground. ∠θ could be within a right triangle (as in the first diagram) or outside a right triangle and greater than 90° (as in the second diagram).

If ∠θ is outside a right triangle, the trigonometry you learned in your last math course can’t be used to calculate the measure directly.

Self-Check 1

Complete questions 1, 2, and 3 on page 83 of the textbook. Answers

Remember that the question asked for an angle rotated in a counterclockwise direction.