Print this chapterPrint this chapter

Lesson 1

1. Lesson 1

1.7. Explore 3

Mathematics 20-1 Module 2

Module 2: Trigonometry

 

Formal Definitions for Primary Trigonometric Ratios

 

You are ready for the formal definition of the primary trigonometric ratios. Don’t worry that the definitions look different from what you learned with right triangles—you’ll soon see how the definitions are compatible with one another.



formula sheet
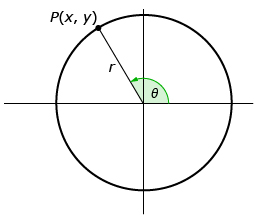
This graphic shows the circle used in the formal definition of the primary trigonometric ratios described above. Point P is shown with coordinates (x, y), the radius is marked as r, and the angle is shown as theta measured from the positive x-axis to the terminal arm.

Given ∠θ drawn in standard position, with P being any point on the terminal arm, the primary trigonometric ratios are defined as follows:

 

 

 

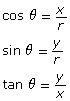
where

  • x is the x-coordinate of point P.
  • y is the y-coordinate of point P.
  • r is the distance from the origin to point P (found by rearranging the Pythagorean formula ).

tip bar

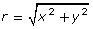Here is a way to help you remember that the definition for cosine uses the x-coordinate of P and the definition for sine uses the y-coordinate of P:

  • Write x and y in alphabetical order and write cosine and sine in alphabetical order.
    •        x,     y
    • cosine, sine

  • Both x and cosine come first, so the cosine definition involves the x-coordinate of P.

  • Similarly, y and sine come second, so the sine definition involves the y-coordinate of P.

When P is on a circle of radius 1, these definitions simplify as follows:

 

 

cos θ = x hint

 

 

sin θ = y hint

 

 

hint

This is a play button that opens Primary Trigonometric Ratios: Formal Definitions.

c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later

Explore these definitions using Primary Trigonometric Ratios: Formal Definitions.



As you may have learned in Try This 1, some interesting facts can be seen using these definitions:

  • When P is on a circle of radius 1, cosine and sine are simply, and respectively, the x- and y-coordinates of P.

  • Equations of the form cos θ = k, where −1 ≤ k ≤ 1, usually have two solutions. The same is true for equations of the form sin θ = k and tan θ = k.

Note that these definitions only use circles—no triangles are required.



caution

Remember that the cosine and sine of an angle are the coordinates of point P only if P is on a circle of radius 1. This is important to remember. Since the radius of the circle can be any value, the radius does not have to be 1.



formula

The formal definitions for primary trigonometric ratios form the foundation of this module. Make sure you have added these formulas and any other information you think will be useful to your copy of Formula Sheet.

 

Self-Check 2

 

This is a play button that opens Primary Trigonometric Ratios: Formal Definitions.

c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later

 



Use Primary Trigonometric Ratios: Formal Definitions to answer the following questions.

  1. Determine the following values:

    1. cos 108° Answer

    2. sin 230° Answer

    3. tan 62° Answer

  2. Determine the two values for θ that will make each of the following equations true:

    1. sin θ = 0.5 Answer

    2. cos θ = −0.4695 Answer

    3. tan θ = −2.4751 Answer
  • Draw a right triangle in standard position with its terminal arm in quadrant 1.

     
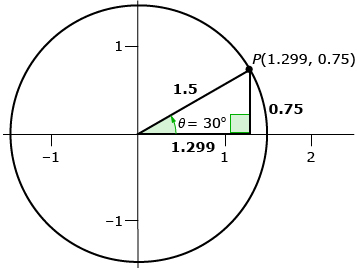
    This is a picture of a right triangle with 30° and 60° angles, embedded within a circle of radius 1.5. The intersection of the circle and the hypotenuse is marked as (1.229, 0.75). The triangle has its 30 degree angle in standard position.

  • Write the tangent ratio you learned in your previous math course,

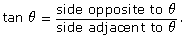
  • The length of the side opposite to θ is the same as the y-coordinate of the endpoint of the terminal arm.

  • The length of the side adjacent to θ is the same as the x-coordinate of the endpoint of the terminal arm.

  • Replacing “side opposite to θ”  to “y” and “side adjacent to x” with “y” results in the definition you learned in this lesson,
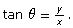
  • Write the sine ratio you learned in your previous math course, SOH for

  • The length of the side opposite to θ is the same as the y-coordinate of the endpoint of the terminal arm.

  • The length of the hypotenuse is 1 since the hypotenuse is the radius of the circle.

Replacing “side opposite to θ” with “y” and “hypotenuse” with “1” results in the definition you learned in this lesson

  • Write the cosine ratio you learned in your previous math course, CAH for .

  • The length of the side adjacent to θ is the same as the x-coordinate of the endpoint of the terminal arm.

  • The length of the hypotenuse is 1 since the hypotenuse is the radius of the circle.

Replacing “Side Adjacent to θ” with “x” and “hypotenuse” with “1” results in the definition you learned in this lesson