Print this chapterPrint this chapter

Lesson 1

1. Lesson 1

1.8. Explore 4

Mathematics 20-1 Module 2

Module 2: Trigonometry

 

You may be wondering how the formal definitions of primary trigonometric ratios are different from what you learned about right triangles in previous math courses. You will investigate this question in Try This 2.

 

Try This 2

 

For angles between 0° and 90°, are the formal definitions for primary trigonometric ratios based on circles different from the definitions based on triangles?

 

 

SUMMARY OF PRIMARY TRIGONOMETRIC

RATIO DEFINITIONS
Ratios Based on a Circle Ratios Based on a Triangle
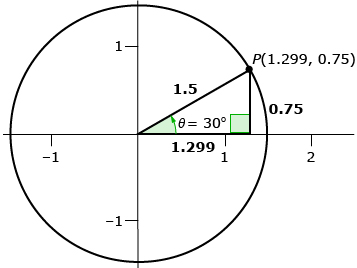
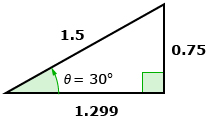
  1. Investigate the sine, cosine, and tangent of a 30° angle. Use the image of the triangle and Primary Trigonometric Ratios: Formal Definitions to complete a table like the following.

     
    This is a play button that opens Primary Trigonometric Ratios: Formal Definitions.

    c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later

    This is a graphic of a right triangle with 30-degree and 60-degree angles. The hypotenuse is labelled 1.5, the side opposite the 30-degree angle is labelled 0.75, and the third side is labelled 1.299.

     
    Trigonometric Function Trigonometric Ratio Based on a Triangle

    Trigonometric Ratio Based on a Circle

    How do you know what length to make the circle radius? answer
    sin 30°    
    cos 30°    
    tan 30°    


  2. How do the trigonometric ratios based on a circle and the ratios based on a triangle compare for sin 30°, cos 30°, and tan 30°?

  3. Explore this relationship further for other triangles using Relation to SOH CAH TOA. Add more rows to your table to record your observations.

    1. Do you think this relationship is true for other angles between 0° and 90°?

    2. Do you think this relationship is true for angles greater than 90°? Explain.

       
      This is a play button that opens Relation to SOH CAH TOA.

      c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later



course folder Save your responses in your course folder.

This triangle can also be drawn within a circle of radius 1.5. So, use a circle with a radius of 1.5.

 

This is a picture of a right triangle with 30-degree and 60-degree angles embedded within a circle of radius 1.5. The intersection of the circle and the hypotenuse is marked as (1.229, 0.75). The triangle has its 30-degree angle in standard position.