Print this chapterPrint this chapter

Lesson 1

1. Lesson 1

1.9. Explore 5

Mathematics 20-1 Module 2

Module 2: Trigonometry

 

The Trigonometric Definitions Are Equivalent

 

As you may have noticed in Try This 2, the formal definitions for trigonometric ratios you’ve just been introduced to and the definitions you learned in your previous math courses (commonly remembered with SOH CAH TOA) are equivalent for angles 0° ≤ θ ≤ 90°.

 

You will get the exact same fractions whether you use a triangle with SOH CAH TOA or a circle with the same radius as the triangle’s hypotenuse and the new trigonometric definitions .

 

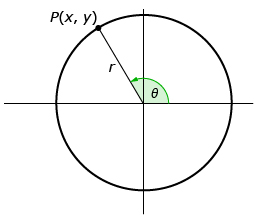
This graphic shows the circle used in the formal definition of the primary trigonometric ratios described above. Point P is shown with coordinates (x, y), the radius is marked as r, and the angle is shown as theta measured from the positive x-axis to the terminal arm.

The definitions of the trigonometric ratios are identical because

  • the side opposite to θ is always the same as the y-coordinate of point P
  • the side adjacent to θ is always the same as the x-coordinate of point P
  • the hypotenuse is always the same as the radius of the circle

With these new definitions of the primary trigonometric ratios, you can revisit the semicircle arch problem from Focus.

 

Example: Boom Angle

 

This is a photo showing the Lune Aqueduct in England.

iStockphoto/Thinkstock

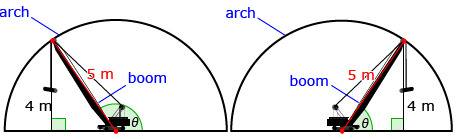
An engineer is working on the restoration of a semicircular arch with a radius of 5 m. As part of the repair, anchors must be installed at a height of 4 m using a special tool attached to a rotating boom. If the boom is positioned in the middle of the arch, at what angle must the boom rotate in a counterclockwise direction so the boom’s endpoint is 4 m off the ground?

 

Solution

 

You saw that there are two places where the boom could be found 4 m above the ground. ∠θ could be within a right triangle (as in the diagram on the left) or outside a right triangle and greater than 90° (as in the diagram on the right).

 

This diagram models the restoration project of a semi-circular arch with radius 5 m. The endpoint of the 4-metre-tall boom is shown perpendicular to the base of the semicircle, once to the left of the boom and one to the right of the boom.

 

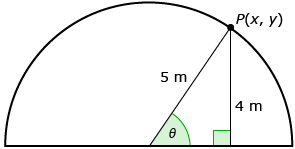
Because the new trigonometric definitions are based on a circle, you can show a slightly different diagram using the new definition for sine:

 

This diagram models the restoration project of a semi-circular arch with radius 5 metres. The intersection of the boom and the semi-circular arch is labelled P with coordinates (x, y). The vertical side leading to the intersection point is 4 metres long. The hypotenuse is 5 metres long (as it is a radius of the semi-circle). The angle between the boom and the base of the triangle is labelled theta.

 

Using the circle-based definition for sine, the calculation is as follows:

 

 

 

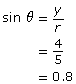
You know from this lesson that there are two solutions to this problem. In other words, there are two angles that make this situation true.

 

This is a play button that opens Primary Trigonometric Ratios: Formal Definitions.

c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later

If you use Primary Trigonometric Ratios: Formal Definitions, you will find that the two values of θ that make this equation true are θ = 54° and θ = 126°. (These are approximate because the applet does not allow for exact solutions.) Check these angles using Primary Trigonometric Ratios: Formal Definitions.