Lesson 2
1. Lesson 2
1.3. Explore 2
Module 2: Trigonometry
The Relationship Between the Solutions and the Axis of Reflection
In Try This 2 you developed three general rules to describe the relationship between the solutions for cos θ = k, sin θ = k (−1 ≤ k ≤ 1), and the axis of reflection. Compare the rules you developed to the following rules.
Cosine Equations
- The terminal arms of the two solutions to equations of the form cos θ = k, where −1 ≤ k ≤ 1, are always reflections of each other in the x-axis.
Sine Equations
- The two solutions to equations of the form sin θ = k, where −1 ≤ k ≤ 1, are always reflections of each other in the y-axis.
Tangent Equations
- The two solutions to equations of the form tan (θ) = a, (a ∈
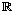) are always reflections of each other in both the x-axis and the y-axis. This always results in the two terminal arms forming a straight line.
Here is a way to help you remember which trigonometric ratio is reflected in which axis:
- The definition for cosine involves the x-coordinate of the endpoint of the terminal arm P(x, y),
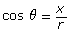. The second solution of an equation like cos θ = k is a reflection in the x-axis.
- The definition for sine involves the y-coordinate of the endpoint of the terminal arm P(x, y),
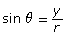. The second solution of an equation like sin θ = k is a reflection in the y-axis.
- The definition for tan involves both the x- and y-coordinates of the endpoint of the terminal arm P(x, y),
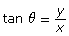. The second solution to an equation like tan θ = k is a reflection in both the x- and y-axes.
The solution method for equations of the form cos θ = k, where −1 ≤ k ≤ 1, used in this resource is significantly different from the method shown in the textbook. Be aware that other strategies exist but that the Self-Check activities in this lesson reflect the solution method presented in this resource.
The relationships described in this section can be used to solve linear trigonometric equations. The next examples illustrate an approach using this knowledge.