Lesson 2

Example 2: Equations of the Form sin θ = k, Where −1 ≤ k ≤ 1

 

David has been asked to solve the equation sin θ = −0.61 to the nearest degree. He knows there must be two solutions to this equation.

 

Step 1: David determines the first solution by entering sin−1(−0.61) in his calculator and rounds the answer to the nearest degree.

 

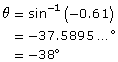
Step 2: How can an angle be negative?

 

In the context of angles in standard position, negative angles correspond to rotations in the clockwise direction. (Up until now, you’ve been dealing with rotations in the counterclockwise direction).

 

 

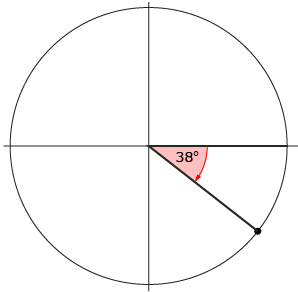
Mathematically, there is nothing wrong with negative angles. However, in the context of Mathematics 20-1, angles are always expressed in their equivalent positive form.

 

Since an angle that is a full revolution is 360°, David concludes that an angle of −38° is equivalent to an angle of 360° − 38° = 322°.

 

David sketches this angle, calling it θ1.

 

 

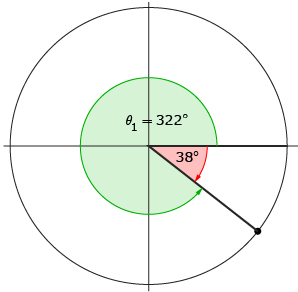
Step 3: He knows that the terminal arm of the second solution, θ2, must be a reflection in the y-axis of θ1’s terminal arm. Therefore, he sketches θ2 with its terminal arm in quadrant 3.

 

 

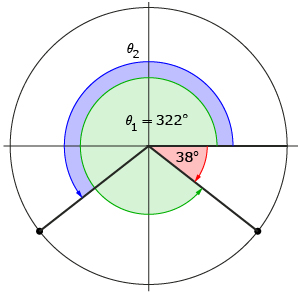
Step 4: Because the terminal arm of θ2 is a reflection in the y-axis of θ1’s terminal arm, David knows the angle between the x-axis and θ2’s angle must also be 38°.

 

 

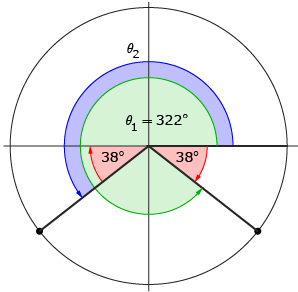
Step 5: David knows that a straight line is an angle of 180° and uses this to determine the second solution:

 

θ2 = 180° + 38° = 218°

 

The two solutions to the equation sin θ = −0.61 are θ1 = 322° and θ2 = 218°.