Lesson 3

1. Lesson 3

1.1. Discover

Mathematics 20-1 Module 2

Module 2: Trigonometry

Discover

Consider the following circle of radius 2 units.

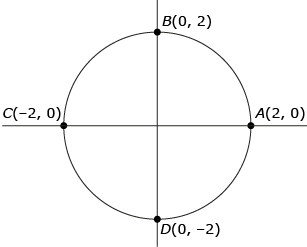
This graphic shows a circle with a radius of 2. The points where the circle intersects the x- and y-axes are marked as A(2, 0), B(0, 2), C(–2, 0), and D(0, –2).

One could imagine superimposing angles in standard position on top of this circle. For instance, this is what a 180° angle would look like:

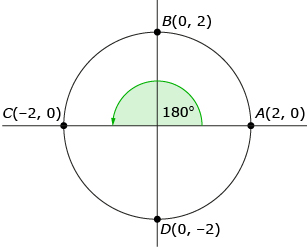
This sketch shows a 180-degree angle in standard position.

Since you know the coordinates of a point on the terminal arm and the distance from that point to the origin (r), you can determine the cosine, sine, and tangent of 180° without technology by using the definitions introduced in Lesson 1.

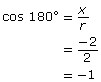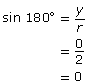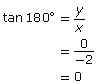Try This 1

Use the definitions process to determine the cosine, sine, and tangent of the following angles.

θ	cos θ	sin θ	tan θ
0°
90°
180°	−1	0	0
270°
360°

Save your chart in your course folder.

Share 1

Compare your results with a partner.

Discuss any differences and try to come to agreement on all values in the table.
How would your values change if the circle had been drawn with a radius of 3 or with any other radius?

If required, save a copy of your discussion in your course folder.

The coordinates of the endpoint of the 270° angle's terminal arm are (0, −2).

Dividing by zero is not valid. Mathematicians say the result is undefined.