Lesson 4

1. Lesson 4

1.6. Explore 5

Mathematics 20-1 Module 2

Module 2: Trigonometry

What you may have concluded is that, depending on the length of CB, there may be zero, one, or two possible triangles whose sides and angle match the given values. The following table summarizes your findings.

In this example, a length of 2.2 for CB can be thought of as a dividing line.

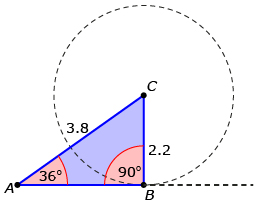
If CB is exactly equal to 2.2, then there is only one triangle possible—a right triangle.

This is a sketch of right triangle ABC. Angle A is 36 degrees, angle B is 90 degrees, side AC is 3.8, and side BC is 2.2. Side AB is on top of a line that is tangent to a circle with radius BC.

c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later

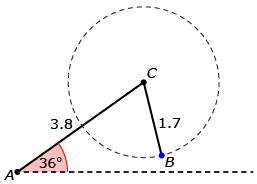
If CB is less than 2.2, there are no possible triangles.

This sketch includes a horizontal dotted line with point A at the left. Point C is positioned so side AC has a length of 3.8 and forms a 36-degree angle with the dotted line. Point C is also the centre of a circle with radius BC. BC is 1.7 units long.

c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later

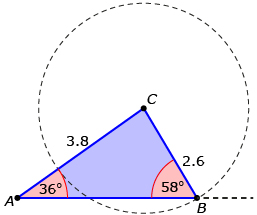
If CB is greater than 2.2 but less than 3.8, there are two possible triangles.

Triangle 1

This is a sketch of triangle ABC. Angle A is 36 degrees, angle B is 58 degrees, side AC is 3.8, and side BC is 2.6. Point C is the centre of a circle with radius BC.

c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later

Triangle 2

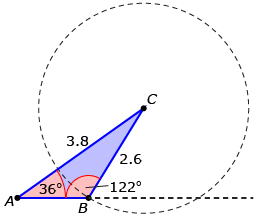
This is a sketch of triangle ABC. Angle A is 36 degrees, angle B is 122 degrees, side AC is 3.8, and side BC is 2.6. Point C is the centre of a circle with radius BC.

c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later

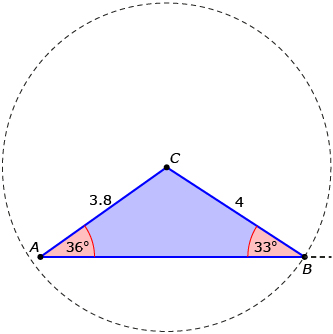
If CB is greater than 3.8, only one triangle is possible.

This is a sketch of triangle ABC. Angle A is 36 degrees, angle B is 33 degrees, side AC is 3.8, and side BC is 4. Point C is the centre of a circle with radius BC.

c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later

This discussion has been in the context of two particular triangles. In order to solve problems in the future, you need to understand how these different cases (zero, one, or two triangles) can result, regardless of what measurements you are given.

The key to understanding this is that the “dividing” point in the above example (a = 2.2) corresponds to a right triangle.

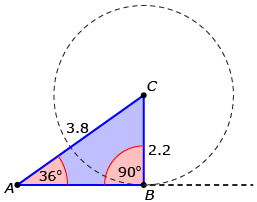
This is a sketch of right triangle ABC. Angle A is 36 degrees, angle B is 90 degrees, side AC is 3.8, and side BC is 2.2. Side AB is on top of a line that is tangent to a circle with radius BC.

c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later

You used Ambiguous Case Explorer to determine the dividing point of 2.2 (side a above). Since a length of 2.2 corresponds to a right triangle, finding the length of a can be easily calculated:

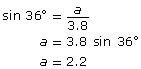
Using standard triangle notation, this can be written as a = b sin A.

Read “The Ambiguous Case,” starting on page 104 of the textbook, for a discussion of how to determine the number of possible triangles for any situation. In this discussion the textbook labels the dividing point as h (because it is the height of a right triangle). Notice that there are two scenarios:

when ∠A is acute
when ∠A is obtuse

“Key Ideas” on page 107 of the textbook provides an excellent summary of the sine law and, in particular, the ambiguous case. Read that section and update your copy of Formula Sheet.

Read “Example 3” on page 106 of the textbook for an example of determining measurements of a triangle when the ambiguous case occurs. Ensure that you understand all the steps before moving on to Self-Check 2.

Self-Check 2

Complete questions 6.a., 6.b., 8.a., 8.b., and 11 on pages 108 and 109 of the textbook. Answers