Lesson 5

Open the Lesson 5 Assignment you saved in your course folder at the start of this lesson. Complete the assignment.

 

Save all your work in your course folder.

 

Project Connection

 

You are now ready to complete the remaining questions, 7 to 11, of Module 2 Project: Mars Rover Simulation.

Save all your work in your course folder.

 

Going Beyond

 

The proof in “Link the Ideas: The Cosine Law” on page 116 of the textbook is only valid for acute triangles. Here is a partial proof for the cosine law for obtuse triangles.

 

 

The first step is to extend AB and draw a perpendicular segment to vertex C.

 

 

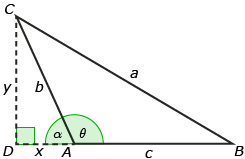
Two expressions can be written using

equation 1:

 

equation 2:  b2 = x2 + y2

 

The Pythagorean theorem can be used again in

 

equation 3: a2 = y2 + (x + c)2

 

Equation 2 can be rearranged to obtain y2 = b2 − x2. Substituting this rearrangement into equation 3 and then simplifying results in the following equation:

 

equation 4: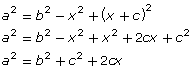

 

Equation 1 can be rearranged to obtain x = b cos α. Substituting this rearrangement into equation 4 results in the following equation:

 

a2 = b2 + c2+ 2bc cos α

 

This is close to the cosine law. If you can show that cos α = −cos θ, then the cosine law results:

 

 

Your task in this Going Beyond is to explain why cos α = − cos θ.

 

Save your response in your course folder.