Module 3

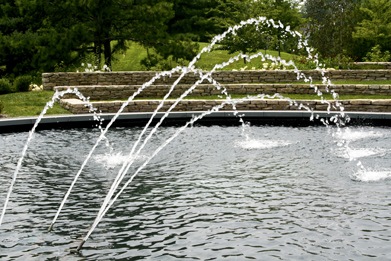
iStockphoto/Thinkstock

 

When water is sprayed in a single stream, the path the water follows is in the shape of a parabola. In this module you will learn that most objects—when they are thrown, shot, launched, or otherwise projected into the air—follow a path in the shape of a parabola. The path of a projectile is called a trajectory. This parabolic path can be modelled using a quadratic function.

 

Jupiterimages/Brand X Pictures/Thinkstock

 

In Module 3 you will learn what a quadratic function is and how to use it to model real-life situations. You will discover that there are two different forms of the quadratic function. Converting between the two forms will help you answer questions about trajectories, structures, and commercial enterprises.

 

You will develop skill at sketching and graphing models of situations that relate to quadratic functions. You will discover more of the capabilities of your graphing calculator, and you will use these capabilities to answer questions and verify results. You will continue to work with quadratic functions in Module 4.

 

In this module you will investigate the following questions:

• How are quadratic functions used to model and analyze problems of projectile motion?
  
  
• How do the parameters of quadratic functions describe the properties of their graphs?

To investigate these questions, you will focus on the lessons and questions in the table.

 

Lesson	Topic	Lesson Questions
1	Investigating Quadratic Functions	How do the values of a, p, and q affect the appearance and placement of the graph of the function y = a(x − p)2 + q?
		What are the characteristics of quadratic functions and their graphs?
2	Quadratic Functions in Vertex Form	How can you sketch a graph of a quadratic function knowing the a-, p-, and q-values?
		How can you write an equation for a quadratic function from its graph?
3	Completing the Square	How do you complete the square to convert a quadratic function in the standard form, y = ax2 + bx + c, into the vertex form, y = a (x − p)2 + q?
4	Properties of y = ax2 + bx + c	How do you determine the characteristics of a quadratic function in the form y = ax2 + bx + c?
		How can you determine whether two functions written in the forms y = ax2 + bx + c and y = a(x − p)2 + q represent the same function?
5	Modelling Problems with Quadratic Functions	How are quadratic functions developed and used to model real-life situations?
		What assumptions are appropriate to model a situation using quadratic functions?

 

The Module 3 Project involves designing a spray park for a playground. You will choose and design a variety of fountain sprays for children to play in and enjoy. You will use quadratic functions to model the paths of those sprays and to design their characteristics.

 

If you start planning your spray park now, you can begin to work on your designs as you work through the lessons. You might want to skip forward and read about the Module 3 Project now.