Lesson 1
1. Lesson 1
1.7. Explore 2
Module 4: Quadratic Equations and Inequalities
Determining the Roots of a Quadratic Equation
In Module 3 you learned about quadratic functions. You learned that a quadratic function is a second-degree expression that can be written in the form y = ax2 + bx + c. A quadratic equation has the same form as a quadratic function and can be expressed as ax2 + bx + c = 0, where a ≠ 0 and a, b, and c are real numbers.
Why is it a condition of quadratic functions and equations that a ≠ 0? ![]()
To solve a quadratic equation means to determine the value(s) of the unknown variable that would make the equation true. The solution(s) of a quadratic equation are known as the roots of the equation.
You can determine the roots of a quadratic equation by analyzing the graph of the corresponding quadratic function. See how you can do this by completing Try This 2.
Try This 2
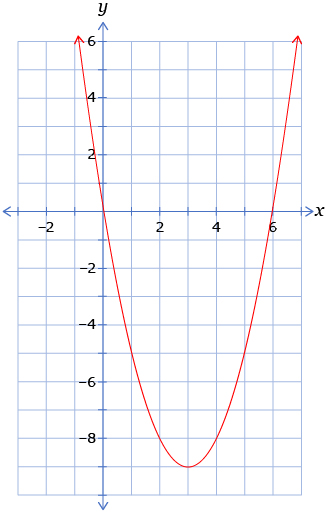
- Consider the quadratic equation x2 − 6x = 0. Use any strategy to find two different values of x that would satisfy the equation. Verify your solutions by substituting the values into the equation and checking that the left-hand side equals 0.
- The graph shows the graph of the quadratic function y = x2 − 6x. Study the properties of the graph. See if you can spot the solutions you identified in question 1 on the graph.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner, respond to the following questions:
- What is the relationship between the roots of the quadratic equation and the x-intercepts of the corresponding quadratic function?
- Check your hypothesis by graphing and solving the quadratic equation x2 + 2x − 15 = 0.
- The x-intercepts of a graph are also known as the zeros of the graph. Give a possible explanation as to why x-intercepts of a graph are called zeros.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Self-Check 1
Work through Distinguishing Between Roots, x-intercepts, and Zeros. You will need to select Solving Quadratic Equations: Using Graphs and then the blue Tutorial button at the top of the window. Finally, select Distinguishing Between Roots, x-intercepts, and Zeros. After working through the applet, make any necessary revisions to your responses to Try This 2 and Share 2.
See what happens when a = 0 is substituted into the quadratic function:
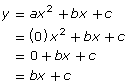
Can you see how this is now a linear equation in the form of y = mx + b? In order to have a quadratic function, the a-value of the coefficient of the x2-term must not be equal to 0.