Lesson 3
1. Lesson 3
1.6. Explore 2
Module 4: Quadratic Equations and Inequalities
Using Square Roots to Solve Quadratic Equations
Recall that the square of any number other than zero is positive. There are always two equal and opposite roots when you take the square root of an equation in the form x2 = a, where a is a real number other than zero.
x2 = a
When x ≠ 0, a > 0.
Applying the square root to both sides of the equation results in
Two equal and opposite sides!
You may have used one of the following strategies to solve the question in Try This 1. Watch Using Square Roots to Solve Quadratic Equations. You will see two ways to solve quadratic equations by taking the square root of the expressions on each side of the equation.
From the video, you can see that when a quadratic equation is in the form (x − p)2 = a, you can use the square roots strategy to determine the equation’s roots. In the previous module you learned that a quadratic function in standard form, y = ax2 + bx + c, can be expressed in vertex form, y = a(x − p)2 + q, by completing the square. You can extend the principle of completing the square to quadratic equations.
Try This 2
- Each quadratic function on the left has been converted to the form y = a(x − p)2 + q by completing the square. Use a similar method to convert the corresponding quadratic equation to the form 0 = (x − p)2 + q.
Quadratic Function
Quadratic Equation
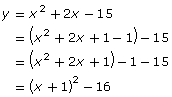
x2 + 2x − 15 = 0
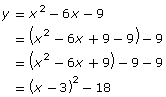
x2 − 6x − 9 = 0
- Working with the completed square (or vertex) form of each quadratic equation in question 1, rearrange the equations into the form (x − p)2 = q.
- Use the square root strategy shown in the video to determine the roots of each quadratic equation.
- Check your answers. Remember that you have learned multiple methods of solving quadratic equations, both algebraic and graphical ones.
Save your solutions in your course folder.
It’s important that you get this one right before moving on. Check your rearrangement:
|
|
