Lesson 3

1. Lesson 3

1.9. Explore 5

Mathematics 20-1 Module 4

Module 4: Quadratic Equations and Inequalities

This shows a photo of a dog kennel with three distinct compartments. There is a dog in one of the compartments.

A dog run is a fenced off area, usually in a yard, where a dog can be confined. A dog run keeps the family pet out of the nicely landscaped yard while still providing ample space for the dog to exercise.

As you already know from the previous lessons, you can model various problems with quadratic equations. You can solve these equations by completing the square. Complete Try This 4 to solve a design problem involving a dog run.

Try This 4

Carmen wants to create a dog run for her three dogs. She plans to fence three distinct areas as shown—one for each dog. In order to save on the cost of chain link fencing, she plans to place the dog run on a concrete pad and position it so that the yard fence can be used as the fourth side. Carmen has 20 m of fencing available. She would like to build a dog run with the greatest area between the house and garage.

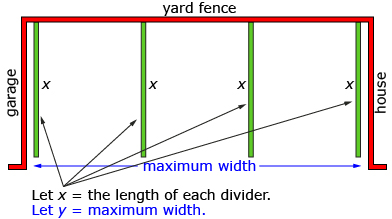
This shows an illustration of the proposed dog run which has been separated into three distinct compartments. Each divider is of length x.

Determine the maximum area of the dog run. What will the dimensions be for each compartment?

If you get stuck, access one of these hints:
- How do I set up the equations?
- What do I do with the equations?
- How do I determine the length?
- How do I determine the width?
- How will I know if I found the correct dimensions?
Suppose the distance between the garage and the house is 9 m. Will Carmen be able to construct a dog run with the maximum area from the previous question? Support your reasoning.

Stuck? Try this hint:
- How do I approach this problem?
Suppose the dog run has an area of 23 m2. For each possible design that satisfies this criteria, determine the dimensions of each compartment.

Hints are available if you need help:
- What equation models this problem?
- How do I solve the equation?
- How many designs should there be?
- How will I know if I got the correct answer?

Self-Check 3

Complete questions 8, 10, and 11 on pages 241 and 242 of the textbook. Answer

The sum of the areas of each compartment equals the
total area, 23 m2.

Notice that your solution should include a positive root as well as a negative root.

This is a quadratic equation, so you can use any appropriate method; but a square root strategy would be convenient.

Set the quadratic expression for area from question 1 to 23.

Compare the width of the design from question 1 with the distance between the garage and the house.

The sum of the areas of the three compartments equals the maximum area.

The width is the maximum area divided by the length.

Complete the square and determine the x-coordinate of the vertex of the quadratic function.

Substitute one equation into the other to get an equation for area in terms of x.

Let x = the length of each divider and let y = the width. Then set up one equation for the area and one equation for the total amount of fencing.