Lesson 4
1. Lesson 4
1.12. Lesson 4 Summary
Module 4: Quadratic Equations and Inequalities
Lesson 4 Summary
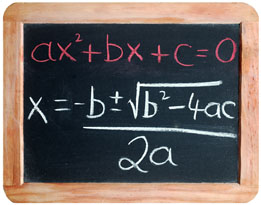
© treenabeena/13191894/Fotolia
In this lesson you investigated the following questions:
- How is the quadratic formula related to the strategy of completing the square?
- How does a mathematical formula reveal the nature of the solutions of a problem?
In this lesson you extended the strategy of completing the square to the development of the quadratic formula. By using the parameters a, b, and c, you were able to generalize a formula that could be applied to the solution of all quadratic equations. For any quadratic equation, ax2 + bx + c = 0, the exact roots can be determined by evaluating ![]() .
.
You discovered that by evaluating the discriminant b2 − 4ac, you could determine the nature of the roots. The following table summarizes these results.
| Discriminant | Nature of Roots |
| b2 − 4ac > 0 | two distinct and real roots |
| b2 − 4ac = 0 | one distinct or two real and equal roots |
| b2 − 4ac < 0 | no real roots |
In the second half of this module, you will study systems of quadratic and linear equations. You will build on what you learned in previous math courses as well as what you have learned about solving quadratic equations. You will work closely with graphs as you complete this module.