Print this chapterPrint this chapter

Lesson 5

1. Lesson 5

1.4. Discover

Mathematics 20-1 Module 4

Module 4: Quadratic Equations and Inequalities

 

Discover
 

The following graphs show the different ways two linear functions can be sketched on the same set of axes.

 

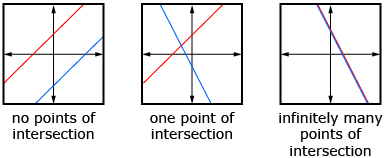
This shows a series of three graphs illustrating the three different ways that a pair of lines can intersect. The first shows no points of intersection (i.e., the lines are parallel), the second shows one point of intersection, and the final graph shows infinitely many points of intersection (i.e., the lines coincide).

 

In Try This 1 you will construct all the ways that quadratic functions and linear functions can be sketched. You will need to use graph paper. You can use Four Grids or use your own graph paper.

 

Try This 1

 

Part A: Linear-Quadratic System

  1. Think about the number of ways that a parabola and a line can intersect on the coordinate plane. For each of the ways this can happen, sketch a possible graph.

  2. Consider the following system of equations:

     
    y = x2 + 4x − 1
     
    y = x + 1

    1. Why do you think this is called a linear-quadratic system?

    2. How many solutions are possible for this system?

    3. How could you determine the solutions?

Part B: Quadratic-Quadratic System

  1. Think about the number of ways that two parabolas can intersect on the coordinate plane. For each of the ways this can happen, sketch a possible graph.

  2. Consider the following system of equations:

     
    y = x2 − 6x + 13
     
    y = –2x2 + 12x − 14

    1. Why do you think this is called a quadratic-quadratic system?

    2. How many solutions are possible for this system?

    3. How could you determine the solutions?

course folder Save your work in your folder.

 

The concepts you have explored here represent the basis of this lesson. You will work with these concepts further in the remainder of the lesson.