Print this chapterPrint this chapter

Lesson 5

1. Lesson 5

1.7. Explore 3

Mathematics 20-1 Module 4

Module 4: Quadratic Equations and Inequalities

 

Relating a System of Equations to a Given Context

 

Now that you have learned how to solve linear-quadratic and quadratic-quadratic systems by graphing, you are prepared to consider how these systems can be related to different contexts.

 

This is a play button that opens Gravity Experiment (Newton's Laws: Summary).

© 1985 California Institute of Technology, The Corporation for Community College Television and The Annenberg/CPB Project

In the next section you will consider a classic physics problem in action. Watch Gravity Experiment (“Newton's Laws: Summary”) to get started.



Share 1

 

With a partner, consider the following systems.

 

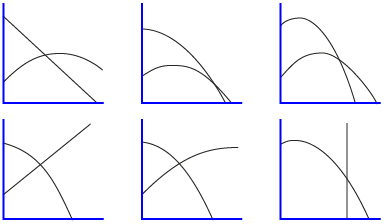
This shows six different graphs relating height to time. Half of the graphs show linear-quadratic systems and the other half show quadratic-quadratic systems.

 

Decide which system would best represent the scenario shown in Gravity Experiment (“Newton's Laws: Summary”). Give explanations to support your choice. Also give reasons to reject the other choices.

 

Example 1: Olympic Springboard Diving


textbook

Turn to “Example 1” on page 427 of the textbook and work through a context similar to the one you experienced in Gravity Experiment (“Newton's Laws: Summary.”) In this case, the context relates to Olympic springboard diving. Look for the answers to the following questions as you read through the problem:

  • In what way is the system represented by this example different from the system in Gravity Experiment (“Newton's Laws: Summary”)?

  • The solution not only gives the reasoning for choosing the graph that represents the system, but the solution also gives reasons for eliminating the graphs that do not represent the system. On what grounds are those graphs eliminated?
Try This 3

 

Julie and Nate are siblings. Julie is older than Nate by 7 yr. The square of Nate’s age 5 yr ago is the same as Julie’s age now.

 

The situation is represented by this system of equations:

 

 

y = x + 7

 

y = (x − 5)2

  1. Explain what the variables in the system represent.

  2. Explain why the system of equations represents the situation.

  3. Solve the system of equations by graphing. How old are Julie and Nate?

course folder Save your work in your course folder.

 

Share 2

 

With a partner, compare your work from Try This 3. Discuss the following points. Record your discussion.

  1. One of the solutions that you obtained from your graph is extraneous. Explain why this solution does not have any meaning in the context of the problem.

  2. How do you know that there could not be any other solution?

  3. If you were not given the system of equations, how would you use the information about Julie’s and Nate’s ages to model the situation?

  4. How could you solve this problem without using a calculator?

course folder Save a copy of your discussion points in your course folder.

 

You will use your discussion notes as you investigate algebraic methods of solving a system of linear-quadratic equations in the next lesson.



There are two possible answers.
Check your answer before moving on. You should have indicated that Julie's age is represented by y, and x is Nate's age.

System A is eliminated because the height of the springboard is shown as changing over time.

 

System B is eliminated because the diver's path is linear, not parabolic.

 

System C is eliminated because the starting height of the diver is different from the height of the springboard.

In the example, the springboard's height remains constant over time; it does not change. In the video, the height of the monkey does change over time as the monkey falls.