Lesson 6
1. Lesson 6
1.8. Explore 4
Module 4: Quadratic Equations and Inequalities
Try This 3
- Consider the following quadratic-quadratic system.
y = 3x2 + x − 2
y = x2 + 2x + 1
Solve this system algebraically by following this example shown for the linear-quadratic system:
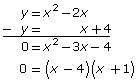
- Reduce the system to a single equation in one variable using elimination.
- Determine the solution(s) algebraically to the resulting equation using an appropriate strategy.
- Verify your solution(s) algebraically.
- Reduce the system to a single equation in one variable using elimination.
![]() Save your work in your course folder.
Save your work in your course folder.
Share 3
- Compare your solution strategies with a partner. Discuss the relative advantages and drawbacks of the strategies for
- reducing the system to a single equation
- solving the quadratic equation
- reducing the system to a single equation
- Why is it difficult to solve this system by eliminating the x-variable instead of the y-variable?
-
- With your partner, manipulate the system so that you can eliminate the x2-term. Graph the resulting equation, as well as the equations in the system.
y = 3x2 + x − 2
y = x2 + 2x + 1
- What do you notice about graphing the equations from part a?
- With your partner, manipulate the system so that you can eliminate the x2-term. Graph the resulting equation, as well as the equations in the system.
- How can a strategy for solving the original system be developed based on your observations from question 3?
![]() Save your work in your course folder.
Save your work in your course folder.
Self-Check 2
Complete questions 3.d., 4.d., 5.a., and 7 on pages 451 and 452 in the textbook. Answer

Hemera/Thinkstock