Lesson 3

You have discovered that adding or subtracting rational expressions is relatively straightforward when the expressions have common denominators. What do you do when the denominators are not common? It is time to learn strategies for evaluating sums and differences of rational expressions with unlike denominators.

 

Adding and Subtracting Rational Expressions with Unlike Denominators

 

To add and subtract fractions with unlike denominators, start by writing the fractions as equivalent fractions over a common denominator. Once the equivalent fractions are obtained, you can apply the same approach you previously used to add and subtract fractions with common denominators.

 

The lowest common denominator (LCD) can be found for any group of denominators using different methods. Retrieve your results from Try This 1. In that activity you explored two methods—the factored form method and the GCF method. Watch Making Equivalent Fractions: Factored Form and Making Equivalent Fractions: GCF × LCM to see these methods in action!

 

Now that you know the lowest common denominator (found using either of the methods in the preceding animations), you can evaluate the sum.

 

Example

 

Evaluate

 

Solution

 

 

Step 1: Find the LCD.

 

The LCD is 60.

 

Step 2: Convert the fractions to the LCD.

 

 

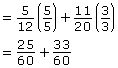
Step 3: Write the expression over one denominator.

 

 

Step 4: Simplify.

 

 

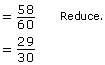
Share 2

 

With a partner, analyze the steps in the example and answer the following questions.

1. Describe the mathematical ideas that are applied at each step.
   
   
2. Explain why, in Step 2, the fractions are multiplied by 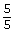and by 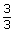, respectively. Why were those particular fractions chosen?

Save your work in your course folder.