Lesson 3
1. Lesson 3
1.9. Explore 5
Module 6: Rational Expressions
Simplifying Rational Expressions with Binomial Factors in the Denominator
The factors of the denominator of a rational expression can be
- a constant
- a monomial
- a binomial
In any of these cases, consider factoring the denominator to its simplest form to help determine the lowest common denominator. Watch Example: Simplifying Complex Expressions to see how you can add and subtract rational expressions with binomial factors in the denominator.
Read through “Example 3” on page 326 and “Example 2.a.” on page 334 to review other instances where you must simplify expressions involving multiple operations on rational expressions. As you work through each example, focus on finding the answers to the following questions:
- In “Example 3,” how do you decide which operation to evaluate first?
- In “Example 3,” what is the relationship between the expression (2m − 3) and (3m − 2)?
- In ”Example 2.a.,” what is the denominator of an expression when a denominator is not given?
- In ”Example 2.a.,” the first term,
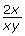, could have been simplified to 
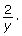What is the danger in doing this at the beginning?
Self-Check 3
Complete “Apply” questions 8, 10, and 15 on pages 336 to 338 in the textbook. Answer