Lesson 1
1. Lesson 1
1.8. Explore 4
Module 7: Absolute Value and Reciprocal Functions
Self-Check 1
- For each of the statements a. to e., indicate which of the following answers (A, B, or C) applies.
- −7
- 7
- neither
- Evaluate the following expression and indicate which answer applies.
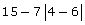
- −16
- 1
- 16
- 29
Answer
- Evaluate the following expression and indicate which answer applies.
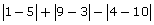
- 4
- 8
- −8
- −4
Answer
- Evaluate the following expression and indicate which answer applies.
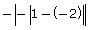
- −3
- −1
- 1
- 3
Answer
Absolute Value and Distance
In the introduction to the lesson you were asked to compare the distance from Edmonton to Calgary, and from Calgary to Edmonton. In fact, the distances are the same and, in both cases, reported as positive numbers. The concept of absolute value is useful in determining distances between numbers on a number line, where the answer is always positive. Study the next example to see two ways to use absolute value to represent the distance between two numbers on the number line.
Example
Determine the distance between the numbers 5 and −1.2 on the number line.
Solution
Method 1: Subtract the smaller number from the larger number.
![]()
Method 2: Calculate the absolute value of the difference of the two numbers.
| Alternative A | Alternative B |
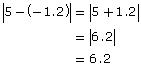 |
Share 1
With a partner, discuss the following questions based on the example. Record your answers and save them in your course folder.
- What are the advantages and one disadvantage of each method?
- In Method 2, why is it not necessary to identify the larger of the two numbers?
![]() Save your responses in your course folder.
Save your responses in your course folder.