Lesson 3

Absolute Value Equations with Extraneous Solutions

 

Retrieve your results from Part B of Try This 1, which you completed in the Discover section.

 

In that exercise, you solved the equation  both graphically and algebraically.

 

Study the next example carefully to see if your results match the solution shown.

 

Example

 

Solve the equation .

1. graphically
   
   
2. algebraically

Solution

1. You can use the same graphical approach as the one you used before.
   
   Enter Y1 = .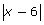
   Enter Y2 = 2x.
   
   You can set your window as x = [−5, 20, 5], y = [−2, 20, 5].
   
   
    
   
   
   

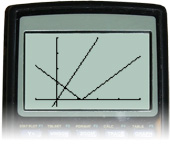
   There appears to be only one solution at x = 2. It is not expected that the graphs will intersect again.
   
   

2. You can use the same algebraic approach as the one you used before.
   
   

   Case 1:  x − 6 > 0
   
   

    

   
   

   
   
   

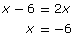
   Case 2: x − 6 < 0
   
   

    

   
   
   

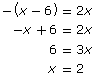
   It appears that there are two solutions to this equation. However, the graphical solution only revealed one root. There may be an extraneous root.

Share 2

 

Complete the tasks and answer the following questions together with a classmate.

1. Verify the roots obtained from the algebraic approach to the previous example.
   
   
2. Which root is extraneous and why?
   
   
3. What other ways could you identify a root as extraneous?

 Record and save your answers in your course folder.