Lesson 4

If a function is defined as y = f(x), then its reciprocal function is . You may recall that a function in this form is considered rational. Remember that rational functions are undefined when the denominator is equal to zero. For instance, consider the function y = x − 1.

 

The reciprocal of this function is . This function is defined except where x − 1 is equal to zero. In other words, this reciprocal function is not defined when x = 1. So what does the graph of a function with a restriction look like? Find out in the next activity.

 

Try This 2

1. Graph the function 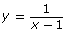 with technology (graphing calculator or other graphing tool).
   
   
2. The function 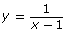 is not defined when x = 1. How does the graph behave at points close to x = 1? What line does the graph approach?
   
   
3. How does the graph behave as x gets larger? As x gets smaller? What line does the graph approach in both cases?

 Record your answers and save them in your course folder.

 

The graph of a reciprocal function will often contain asymptotes. An asymptote is a line that a curve or graph approaches but never touches. Vertical asymptotes occur where the domain is restricted, as you saw in Try This 2. Horizontal asymptotes occur along the x-axis.

 

In the next exercise, you will use a table to manually graph a reciprocal function.

 

Try This 3

 

Consider the function y = x. The reciprocal of this function would be , where x ≠ 0.

1. Complete a table like the one that follows.
   
   
    

   x	y = x ordered pair, ( x, y)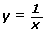	ordered pair, ( x, y)
   −3
   −1
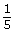
   0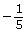
   1
   3

   
   
   
2. Use the ordered pairs from the table to graph y = x and 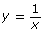 on the same set of axes. Differentiate the two graphs by using different colours.
   
   
3. Verify your graphs from question 2 on a graphing calculator.
   
   
4. State the properties of each function.
   
   
    

   	y = x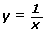
   Domain
   Range
   x-Intercept
   y-Intercept

    

 Save your answers in your course folder.

 

Share 1

 

With a classmate, discuss the following questions. Record your answers.

1. What kind of expression is the reciprocal function?
   
   
2. The denominator of 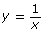 cannot be equal to zero. How does this restriction affect the domain on the graph? What is the behaviour that is exhibited at values close to x = 0?
   
   
3. Explain what happens to the graph as x-values
   
   
   1. increase
      
      
   2. decrease
      
      
4. The graph of  will never touch the x-axis. Explain why.
   
   
5. Discuss advantages and disadvantages of using a table to graph the reciprocal of a function.

 Save your results in your course folder.