Lesson 4

Before you develop a strategy for sketching a reciprocal function based on the principles you discovered earlier, you can practise graphing by using technology.

 

Try This 4

 

Consider the function f(x) = x2− 4.

1. Graph y = f(x). Use the window settings x:[−6, 6, 1], y:[−5, 10, 1]. Capture a screenshot image of the graph, and save it in your course folder; or make a sketch of the screen and save the sketch.
   
   
2. Now graph the function 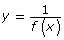. Note the properties of the function. Capture a screenshot image of the graph, and save it in your course folder; or make a sketch of the screen and save the sketch. Write down any questions you may have about what you see.
   
   
3. Watch the Graphing Reciprocal Functions video to see how you can sketch an accurate graph of a reciprocal function without technology. Be sure to pay attention to the three steps that are outlined. Focus on the following questions:
   
   
   • What is the acronym that is used to graph reciprocal functions? What do each of the letters represent?
     
     
   • How are the properties of reciprocals related to the properties of reciprocal functions?
   
   
    
   

Share 2

 

Discuss the following questions with a classmate.

1. Name the properties of reciprocals that you explored in the Discover section.
   
   
2. How are the properties of reciprocals related to the graphs of reciprocal functions?
   
   
3. How can you improve upon the A.I.M. method for graphing reciprocal functions? What would you add, delete, or revise?