Section 1

1. Section 1

1.16. Explore

Mathematics 20-3 Module 2

Section 1: Simple and Compound Interest

Explore

In Discover you may have noticed the following differences between simple interest and compound interest.

Simple Interest	Compound Interest
This is calculated only on the original principal.	This is calculated on the interest earned and the principal.
Interest earned is not reinvested. Therefore, it is not used in interest calculations for following periods.	Interest earned during the previous period is added to the principal. This total will become the new principal and all the money will earn interest.
The applet called Simple Interest Versus Compound Interest, which you used in Discover, calculated the simple interest over five years but, in reality, simple interest is normally used for short-term loans of 30 or 60 days.	For long-term loans, compound interest is used.

Did You Know?

Richard Witt’s Arithmeticall Questions, published in 1613, was one of the first books in the English language that contained detailed tables and formulas for calculating both simple and compound interest. You will be using Witt’s formula for compound interest later in this lesson. To apply this formula, you will need your exponent skills! The following illustration is a question on compound interest from Witt’s book.

This graphic is a question on compound interest described in Richard Witt’s 1613 book titled Arithmeticall Questions.

In Try This 1, both investments are calculated annually—for simple interest this is always the case, so time must be converted to years. However, compound interest may be paid out more than once a year, even though the interest is quoted as annual interest. These shorter periods of time where interest is paid out are called compounding periods.

Due to compounding periods, the compound interest formula is a bit more complicated than simple interest.

A is the final amount of the investment.
P is the principal.
r is the annual interest rate.
n is the number of compounding periods in a year.
t is the term in years.

This is a photo of Ravia.

iStockphoto/Thinkstock

Example

Ravia lives in Fort Vermilion, Alberta. She has just invested $1000 in a five-year, compound interest bond. The annual interest rate is 6%, compounded annually. Use the compound interest formula to see how much her investment will be worth in five years.

Solution

Identify the variables from the question.

P = $5000

r = 6% = 0.06

t = 5

n = 1

Substitute the known variables into the compound interest formula to find the final amount of the investment (A).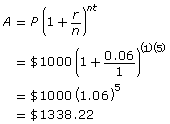