Section 1

Discover

 

In this section you will discover how to quickly estimate the time required to double an investment at a given rate of compound interest.

 

When Oscar entered Grade 1, his grandmother invested $2000 towards his education. The money was invested at 8% compounded annually over 12 years. This year, Oscar will use this money when he attends the First Nations University of Canada at Regina.

 

The following spreadsheet tracks the growth of this investment over 12 years.

 

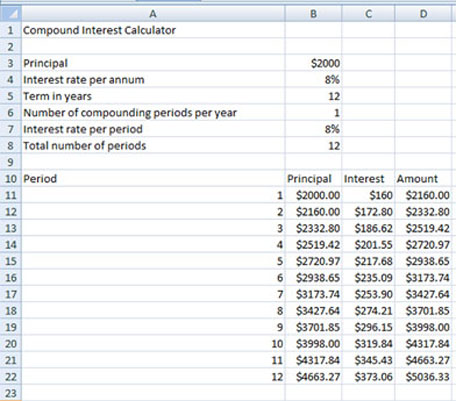
© Microsoft Corporation. All Rights Reserved. Used with permission from Microsoft Corporation.

 

Try This 1

1. At the end of which investment year does the original $2000 double in value?
   
   
2. Divide the number 72 by your answer to question 1. How does this answer compare to the interest rate of this investment?
   
   
3. The answer to question 2 illustrates the Rule of 72. Can you suggest what is meant by the Rule of 72?
   
   
4. About how many years would it take an investment to double in value at 6% compounded annually? Why?

Save your answers to your course folder.

 

Share 1

 

Share your responses to the questions in Try This 1 with a classmate or group.

• How did your interpretation of the Rule of 72 compare with the opinions of other students?
  
  
• Why might there have been similarities and differences between the interpretations?

If required, save a copy of your discussion in your course folder.