Print this chapterPrint this chapter

Section 1

1. Section 1

1.17. Explore 2

Mathematics 20-3 Module 3

Section 1: Slope—Physical Objects

 

Self-Check 1

 

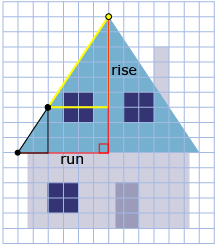
The illustration is of a house. Along the roof line is a large, yellow triangle.

 

  1. Calculate the slope between two different places on the diagram above.

    1. Calculate the slope of the line between the black points. Use the black triangle to find the rise and run. Answer

    2. Calculate the slope of the line between the yellow points. Use the yellow triangle to find the rise and run. Answer

  2. How do the two slopes on the same line compare? Answer

Refer back to Discover. What patterns did you discover for the slope of lines? You may have noticed that the slope of a curved line changed. The slope on the curved line depended on where you measured the rise and run on the curve. This slope was very different than the slope of a straight line. The slope of a straight line is the same no matter where you measure the rise and run. This slope is called a constant slope.

 

A straight line has a constant slope. A curved line does not.

 

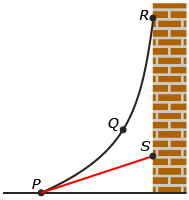
The illustration is of two attachments to a wall. One attachment is a cable that takes a curved shape. The other attachment is a red metal bar that is a straight line.
Self-Check 2

 

Answer true or false to questions 1 and 2.

  1. Line segment PS would have a constant slope. Answer
  1. Line segments PQ, QR, and PR would have different slopes. Answer
  1. Calculate the slope of PS. How did you calculate the slope? Answer