Section 1

Explore

 

In Focus you saw that water slides come in all shapes and sizes. You also thought about the factors that determine how steep the slides are. In Discover you began to calculate the slopes of two water slides, and you may have noticed a similarity between them. The rise of one slide was equal to the run of the other.

 

The steeper green slide has a slope of and the shallower blue slide has a slope of . You may have noticed that the larger the slope value, the steeper the slope.

 

A water slide is a slippery slope. You don’t want your roof to be a slippery slope.

 

Carpenters refer to a roof’s slope as the pitch. Many factors influence how steep a roof is built. The pitch of a roof is found by measuring the amount the roof rises for every 12 in, or 1 ft, of run.

 

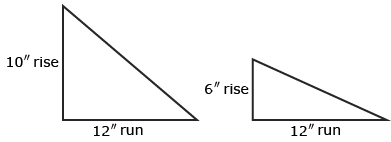
Compare the two roof pitches in the following graphics. The runs are both 12 in, so the rise is what determines the slope’s steepness. The pitch (a 10-in rise for every 12-in run) is much steeper than the roof pitch. When the run length is kept standard (12 in), what determines the roof's steepness? It's the rise: the higher the rise, the steeper the slope.

 

 

Example

 

In the activity Roof Pitch, the pitch is calculated using a grid.