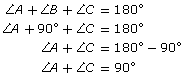Lesson 2

Explore

 

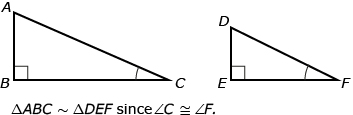
In Discover, the two right triangles you used were similar because one pair of acute angles were equal in measure.

 

Suppose you had two right triangles, , and in those triangles . Then, .

 

 

The reason is based on the principle that in a right triangle, the two acute angles must add up to 90°.

 

For ,
Because angle B is equal to 90°,   the two acute angles, A and C, must also equal 90°.
For example, if ∠C = 40°, then ∠A must be 50°.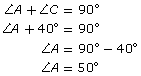
Since the two triangles are similar, the corresponding angles will be the same.	∠F = 40° and ∠D = 50°

 

Try This 2

 

Jonathan walked 15 m from the wall of his apartment building. At that point, he noticed that his shadow reached the same point on the ground as the building’s shadow. If Jon is 1.6 m tall, and his shadow is 3 m long, how high is the apartment building? Round your answer to one decimal place.

1. Sketch and label a diagram to represent the problem.

Watch the steps involved in solving this problem in the Apartment Shadow Problem. On the final slide of the animation, you will set up the proportion needed to solve this problem.

2. Solve the proportion to find out how high the apartment building is.

Save your responses in your course folder.