Lesson 4
1. Lesson 4
1.7. Explore 3
Module 4: The Right Kind Of Triangles

Digital Vision/Thinkstock
Check out another problem situation that can be solved using two triangles. Can you think of another situation where two triangles might help solve a problem?
Example
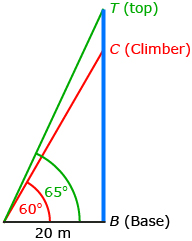
From a point 20 m from the base of a vertical ice wall, the angle of elevation of a climber is 60°. From the same point, the angle of elevation of the top of the wall is 65°. How many more metres must she climb to reach the top? Round to one decimal place.
Solution
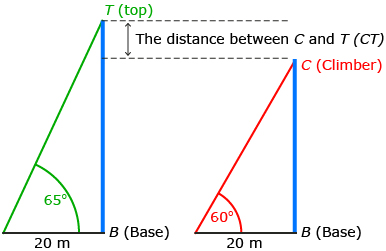
| Draw and label a diagram to represent the problem. |
|
You must determine the distance between C and T. |
CT = BT − BC
|
First find BT.
Use the larger right triangle with the 65° acute angle.
Don’t round until you have made your last calculation. |
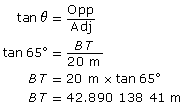 |
Next, find BC.
Use the smaller right triangle with the 60° acute angle. |
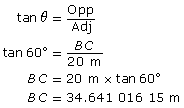 |
Now find the distance CT. The climber has approximately 8.2 m to reach the top. |
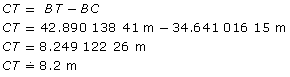 |
If you would like to review another example of a problem that uses two triangles in the solution, turn to page 172 of MathWorks 11 and work through “Example 2.”
Self-Check 2
- Turn to page 177 of MathWorks 11. Do “Build Your Skills” question 1. Answer
- Turn to page 178 of MathWorks 11. Do “Build Your Skills” question 4. Answer
- Turn to page 179 of MathWorks 11. Do “Build Your Skills” question 6. Answer
It is now time to add new math terms and notes to Mathematics 20-3: Glossary Terms.
In this lesson the new terms and notes you will add are
- solving a right triangle
- parts of a triangle