Lesson 5

1. Lesson 5

1.6. Explore 2

Mathematics 20-3 Module 4

Module 4: The Right Kind Of Triangles

Now you will work through an example similar to the problem you encountered Try This 2. The example may help you with any difficulties you had in Try This 2.

Example

Jasmine is 50 m from an intersection with a straight road. Down the road is a power pole. Jasmine must turn to her left through an angle of 30° to measure angle of elevation of the top of the pole. If the angle of elevation of the top of the pole is 5°, to the nearest tenth of a metre, how high is the pole?

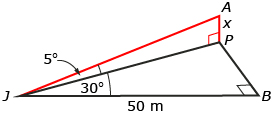
This is an iIllustration of a power pole and dimensions to measure its height.

Read through the following written solution, or watch the video solution, titled Jasmine’s Angle of Elevation.

Video Solution

Written Solution

Determine the length of JP, Jasmine’s distance from the pole.

Using triangle JPB,

JP is the hypotenuse
JB, the adjacent side, is 50 m

From SOH-CAH-TOA, use the cosine ratio.

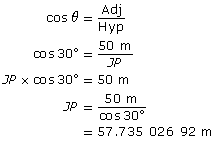Use triangle AJP to find the height of the pole.

Let AP, or x, be the height of the pole; it is the side opposite the 5° angle.
JP is the adjacent side.

From SOH-CAH-TOA, use the tangent ratio.

The pole is approximately 5.1 m tall.