Lesson 1

Explore

 

In previous mathematics courses, much of your work with area has involved two-dimensional shapes. In this lesson your focus will be on the surface area of three-dimensional objects. As you may have noted in Discover, the surface area of a 3-D solid is the sum of the areas of all the solid's sides, faces, or exposed surfaces.

 

In Lesson 1 you will explore the surface area of a variety of different 3-D solids. You will begin by exploring the surface area of cylinders, such as the round bales shown in the photo.

 

Try This 2

 

To prevent spoilage in feed for animals, one option for farmers is to create silage bales. A silage bale is a cylindrical bale of hay or grain covered in plastic. This covering prevents weathering and creates silage, partially fermented feed. Silage is rich in nutrients and can be used as feed during winter. Bales range in size, but you can assume the bales in the photograph are 5 ft in diameter × 5 ft long.

 

To know how much plastic to buy for the silage, the farmer must first know the surface area of each bale.

 

One way to determine the surface area of each round bale is to draw a net.

 

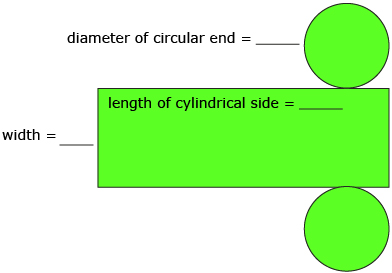
1. Fill in the values for width and diameter on the net diagram.
   
   
2. How is the length of the cylindrical side related to each of the bale’s circular ends? Calculate this length, and fill in the information on the net.
   
   
   
   

3. Calculate, in square feet, the area of the side (the rectangle) of the bale. Round to one decimal place.
   
   

4. Find the area of each circular end of the bale. Round your answer to one decimal place.
   
   
5. Determine, to one decimal place, the bale’s surface area.
   
   
6. Use the surface area of a cylinder formula 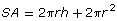to check your answer to question 5. How do your answers compare?
   
   
7. If the farmer has 100 bales, how much plastic will need to be purchased? Round your answer to the nearest square foot.

Save your work in your course folder.