Lesson 1

The following example explores the surface area of a triangular prism. Before you read through the example, use the Exploring Surface Area, Volume, and Nets applet from Try This 3 to view the net and the surface area formula for a triangular prism.

 

Example

 

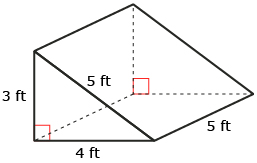
Anton and Xera have volunteered to paint over the graffiti on a skateboard ramp. They took measurements of the ramp and noticed that the top, back, and two sides could be approximated by a triangular prism.

 

Xera and Anton sketched the prism and used the information to calculate the surface area they need to paint. They plan to give the ramp two coats. What is the total area that they must buy paint for? Note: The bottom will not be painted.

 

iStockphoto/Thinkstock

 

Solution

 

Draw the net with dimensions showing the four sides that need to be painted.

 

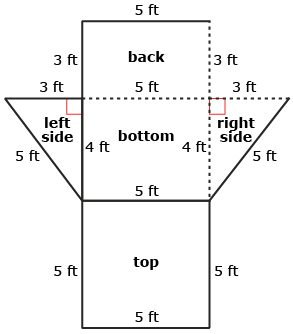
SA = (area of rectangular back) + (area of square top) + (2 × area of triangular side)

 

 

 

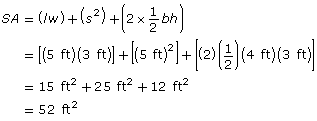
Since Anton and Xera want to apply two coats of paint, they need to buy enough material to cover an area of 2 × 52 ft2 = 104 ft2.

---